 |
 |
Guidelines
for assessing the reliability of 40Ar/39Ar
plateau ages: Application
to ages relevant to hotspot tracks
|
 |
“Therefore
O students study mathematics and do not build without
foundations”
Leonardo da
Vinci, ca. 1500 |
Abstract
The literature contains numerous
40Ar/39Ar
“ages” that, based on statistical
tests, have no geological significance. Herein, I
set out some simple guidelines to permit readers to
assess the reliability of published ages. The emphasis
is on 40Ar/39Ar
data on whole-rock material, though the methods
are applicable to all published plateau data. I illustrate
the use of the techniques by looking at published
age data for hotspot tracks in the Atlantic Ocean
(the Walvis Ridge), as well as newly published ages
for the British Tertiary Igneous Province.
Introduction
The proliferation of 40Ar/39Ar
dating laboratories has led to a large number
of papers reporting age data. However, in many instances,
the published “ages” have no merit, as
they fail the simple statistical tests that should
be applied to all such data. Herein, I consider results
of 40Ar/39Ar
step-heating studies only. In these experiments,
a sample is heated in steps of increasing laboratory
extraction temperature, until all the argon is released.
The argon released in each step is measured to calculate
a “step age” with an associated analytical
error. At the end of the series of experiments, the
step ages (± one sigma errors are quoted herein)
are plotted against the cumulative amount of 39Ar
released. The resulting figure is called an age spectrum
(e.g., Figure
1). This approach is designed to look at
the gas released from sites of increasing
argon retentivity. When a reasonable number of consecutive
steps, carrying a substantial amount of the total
argon released, give the same age, the resulting average
value carries geological significance. For unmetamorphosed
igneous rocks, the latter would normally represent
the crystallization age.
An adjunct method of evaluation is
to present the relevant data on an isotopic ratio
plot and look for straight-line segments through three
or more consecutive heating steps. This is the isochron
technique (see York, 1969; Roddick,
1978; Dalrymple et al., 1988 for details).
Whether the data are evaluated in spectrum or isochron
form, they must pass relevant statistical tests for
“reliability”. These tests are outlined
herein. In earlier work (Baksi, 1999, 2003),
I set out guidelines for assessing the reliability
of 40Ar/39Ar
ages based on critical evaluation of isochron diagrams.
This work followed the first efforts (Brooks et
al., 1972) to distinguish isochrons from “errorchrons”
– the latter occuring where “geological
error” was present and negating the use of the
age for geological purposes. In evaluating 40Ar/39Ar
data on isochron diagrams, the data must be
subject to straight-line fitting (e.g., York,
1969). The resultant “goodness of fit”
parameter, in tandem with the number of points on
the line, must be evaluated for statistical reliability
(95% confidence level generally) using Chi Square
Tables (e.g., deVor et al., 1992).
If the data scatter badly around the best-fitting
straight line, the resulting “age” should
be rejected as being not reliable.
An easier method is to look at the
data on age-spectrum plots and assess the reliability
of “plateau” sections. Though definitions
of what constitutes a plateau vary, a general guideline
is that such sections of the age spectra should contain
at least three consecutive steps, carrying
> 50% of the total 39Ar
released, whose ages “overlap”.
It on this last issue that I shall focus. Two steps
can never define a plateau, and such data cannot be
evaluated on an isochron diagram. Any two points in
the universe lie on a straight line! In evaluating
isochron “goodness of fit parameters”,
the number of degrees of freedom for Chi Square Tables
is N-2, and for two steps, this is zero.
I look primarily at age spectra and
note that plateau sections represent steps that “overlap”
using (40Ar/36Ar)initial
= 295.5 (the atmospheric argon value) for data reduction.
I note that cases where:
-
(40Ar/36Ar)
initial > 295.5, (excess 40Ar
argon is present), are taken care of by isochron
plots, and
-
(40Ar/36Ar)
initial < 295.5, are “disturbed samples”,
e.g., partial loss of (radiogenic) 40Ar*
(formed by in situ decay of 40K)
(Lanphere & Dalrymple, 1978), and the
resultant “age” has no geological significance.
All errors herein are given at the
1-sigma level. For plateau ages, I list the standard
error on the mean (the SEM).
Methodology
The basic principle involved is to evaluate critically
how much the step ages on the plateau differ
from one another. This is done by calculating
the relevant Mean Square Weighted Deviate (MSWD =
F). This parameter measures the scatter of
the individual step ages, with their associated errors
(ti ± dti), from the
mean.
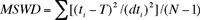
where
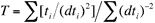
is the mean (the “plateau”
age) and N contiguous steps are used.
It is important to understand that
the MSWD value obtained either from the age-spectrum
plot or the isochron must be used along with the number
of steps for assessing reliability using Chi
Square Tables. Two parameters are used in such
a test. The first
is the number of “degrees of freedom”
of the data set (nu) which is equal to N-1 for plateau
calculations and N-2 for isochron (straight line fitting)
purposes. The second
is the Chi Square value, which is equal
to MSWD multiplied by nu. When the relevant Chi Square
Tables (e.g., deVor et al., 1992) indicate
that the probability of occurence is < 0.05 (95%
confidence level), the “age” (plateau
or isochron) should be rejected. Significant error
is then present, rendering the number (the “age”)
and its associated error estimate geologically meaningless.
As will be demonstrated herein, many “ages”
have been presented in the literature wherein the
relevant statistical tests demonstrate that the probability
of having obtained a statistically meaningful age
is not only < 0.01 (1%), but often < 0.000001
(10-6).
I begin by noting that Brooks
et al. (1972), in their treatment of geochronological
data, suggested rejection of straight lines as isochrons
when MSWD > 2.5. For data with thenumber of degrees
of freedom (nu = N – 2) = 1, 3, 5,
10 the corresponding probability values are 0.11,
0.06, 0.03 and 0.005, respectively.
Note that the same value of MSWD
(= 2.5), makes an isochron statistically acceptable
for up to 5 points (nu = 3), but unacceptable when
seven or more points are used (nu > 5). This is
of particular importance today, when age spectra often
contain 10 – 20 steps. Clearly each case must
be evaluated individually for “statistical reliability”.
I begin by looking at a hypothetrical data
set. Consider a case of five steps carrying
equal quantities of gas giving rise to step
ages of 99.0, 101.0, 100.0, 101.0 and 99.0
Ma, each with an error of ± 0.5 m.y.
The plateau age of 100.00 Ma, with a standard
error on the mean:
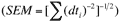
of ± 0.22 Ma is found to be unacceptable,
with p ~ 0.003 (Figure
1).
|
Visually,
there appear to be fairly minor “bumps”
on the plateau section, but no proper estimate
of the crystallization age can be made from
this age spectrum. The crystallization age may
lie between ~ 99 and 101 m.yr. However, its
exact value, and equally important its error
estimate, cannot be stated with statistical
confidence. When other age spectra show steps
deviating markedly from each other i.e., much
more severe “bumps”, clearly
no plateau section has been developed. This
will be considered in detail for two specimens
below. |
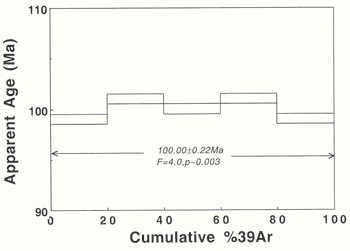
Figure
1: Age spectrum plot for hypothetical data set |
In the above instance (Figure
1), if each step age error were ±
1.0 m.y., the corresponding p value would
be ~ 0.41, making the plateau age (100.00 ±
0.45 Ma) acceptable as a crystallization value. Step
age errors must be estimated/calculated properly.
Errors in isotopic ratio measurements must be used
correctly (see Dalrymple et al., 1981) to
calculate step age errors. In particular, sigma-j,
the estimated error in determination of the irradiation
parameter, must NOT be used in (each) step age error
calculation.
It has been pointed out by Roddick
(1978) that in instances where the MSWD > 1, the
calculated error in the plateau should be multiplied
by (MSWD)1/2. I will follow this procedure
only when the plateau is statistically acceptable
(p > 0.05). In cases where MSWD is very
large (e.g., > 10), such multiplication
of the plateau age error, would make the age “less
precise” and may be thought to be functionally
usable. However, if p < 0.05, the probability
of the steps defining a proper plateau are unacceptable.
Estimating its age with a less precise “number”
is to be avoided.
In evaluating age spectra sections
thought to make up plateau sections, nu = N-1. I illustrate
the use of this technique for data taken from the
literature. I presume that the relevant data sets
(step ages with associated errors, or preferably measured
isotopic ratios with associated errors) are either
available in tables within the paper, at a supplementary
site, or will be supplied by the authors. Since it
is not desirable to reinterpret all published data,
I offer some guidelines for data sets that are worth
closer inspection.
Look for the following:
-
where the relevant MSWD value
is not quoted,
-
where the figures are not drawn
to an ideal scale (see example below), and
-
where step ages often differ
by more than the relevant 95% confidence value amount
(see Baksi, 1999).
The significance of i. above is self-evident. If
the MSWD value is not quoted, it can easily be calculated
and used in conjunction with Chi Square Tables to
assess reliability. Point ii. is illustrated in Figure
2. The apparent age may be drawn on
a far-from-ideal scale, precluding quick visual evaluation
of the “plateau” (Figures
2a, b). The same data sets are redrawn
to a proper scale in Figures
2c and 2d.
Visual inspection suggests a plateau may be developed
for the RT sample (Baksi, 2001), but not
for LB1 San (Chambers & Pringle, 2001),
wherein the age spectrum shows severe bumps. Proper
statistical evaluation confirms this. Note that in
Figure 2c
the last four or five steps may be taken to define
a plateau. The two sets of plateau ages (see Figure
2c) overlap statistically. Four steps
were used to define the plateau age by Baksi
(2001), noting slight loss of 40Ar*
(lower ages) at both the lowest and highest temeprature
steps.
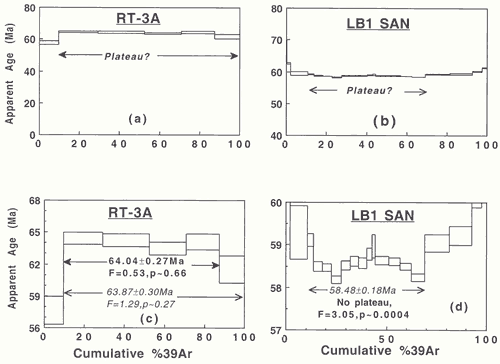
Figure
2: Examples of acceptable (left) and unacceptable
(right) age spectra where relevant details of the
plateau sections are obscured by use of inappropriate
apparent age scales (top panels).
Point iii. above forms the main focus
of this webpage and is illustrated below using examples
taken from the literature. I briefly consider age
spectra where low temperature steps yield older ages
than those at higher temperatures. The former
and latter derive gas from low and high argon rentention
sites respectively. Thus low-temperature steps normally
exhibit ages lower than, or equal to, those of the
higher temerature steps. “Descending staircase”
type age spectra may result from two totally different
phenomena. The first is due to the presence of excess
40Ar in the
rock, which is often released preferentially to 40Ar*
at relatively low temperatures. The second explanation
involves 39Ar
recoil within the sample. Prior to laboratory heating
of the rock, during irradiation of the sample in a
nuclear reactor, a fast neutron enters the 39K
atom, converting it to 39Ar, as
a proton is released (fired out). Like the recoil
of a gun when a bullet is fired, the 39Ar
formed by the reaction, recoils. In this process,
it may move from one mineral phase to a contiguous
one, creating a “disturbed” age spectrum. Examples
of both phenomena (excess 40Ar
and 39Ar recoil)
are given in Baksi (1994) and references
cited therein.
Case Histories
(1) Examination of ages reported for whole-rock
basalts from the Walvis Ridge, Atlantic Ocean.
| O’Connor
& Duncan (1990) reported a number of
“plateau ages” to temporally define
the track of the Tristan da Cunha hotspot. These
ages were subsequently used by Muller et
al. (1993) to derive plate motions relative
to hotspots. Based on evaluation of isochron
plots for each specimen Baksi (1999)
showed that almost all the ages were untenable
as crystallization values. In this web page,
I take a similar approach (but one that is somewhat
easier to visualize) to evaluate these ages
based on their age spectra. |
|
In Figures
3 – 6 plateau ages as
reported by O’Connor & Duncan
(1990) are shown in italics, and the proper
statistical evaluation is shown in bold (F
= MSWD value, p = probability of occurrence
based on Chi Square Tables, using the appropriate
number of degrees of freedom). All the samples
dated by O’Connor & Duncan
(1990) were whole-rock basalts.
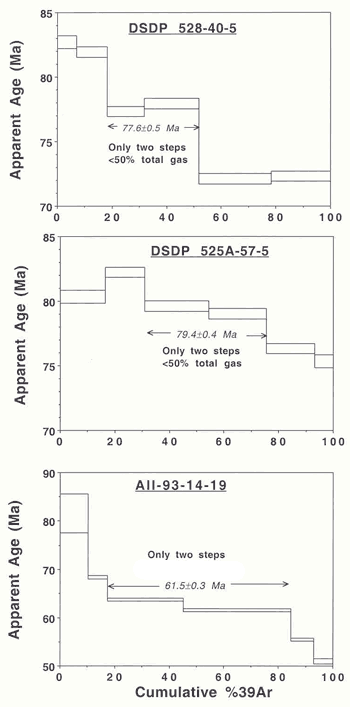
DSDP 528-40-5/525A-57-5,
AII-93-14-9: Age spectra are shown
in Figure 3.
The first sample shows a descending-staircase
type of age spectrum. Based on only two steps
O’Connor & Duncan (1990)
reported a plateau age of 77.6 ± 0.5
Ma. This is by definition untenable.
Similar two-step plateau ages of 79.4 ±
0.4 Ma and 61.5 ± 0.3 Ma (O’Connor
& Duncan, 1990) for specimens DSDP
525A-57-5 and AII-93-14-9, are also rejected.
Baksi (1999) showed that the isochrons
(ages) reported by O’Connor &
Duncan (1990) for the two DSDP specimens
show MSWD > 100; p <10-10.
For the third specimen, the isochron (for all
six steps) used by O’Connor &
Duncan (1990), yields MSWD > 1000 (Baksi,
1999) and p < 10-20.
None of these specimens yields an age (plateau
or isochron) sufficiently accurate to be utilized
for tracing hotspot tracks.
Figure
3: Age spectra for disturbed samples from the
Tristan da Cunha hotspot track (the Walvis ridge). |
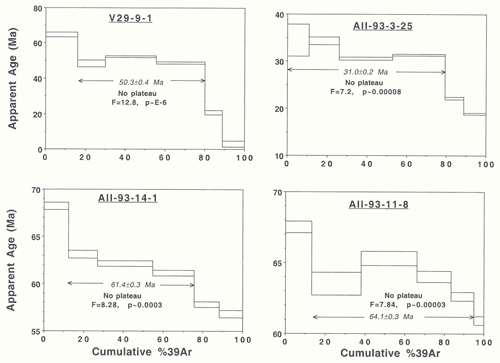
Figure
4: Age spectra showing older apparent ages for low-temperature
steps than for high-temperature steps.
V29-9-1, AII-93-3-25/93-14-1/93-11-8:
Age spectra are shown in Figure
4. The plateau ages reported by O’Connor
& Duncan (1990), are untenable because of
very high MSWD values. The corresponding p
values are all < 0.0005. These descending staircase
age spectra may indicate the presence of excess 40Ar.
For this reason (see Introduction above) the corresponding
isochron plots need to be critically examined. Baksi
(1999) showed that the MSWD values for these straight
lines are 36, 5.5, 6.2 and 60 respectively. The corresponding
probability values are < 10-6, 0.004,
0.012 and <10-20, respectively. These
four specimens gave no plateau/isochron ages that
can be utilized for delineating hotspot tracks in
the South Atlantic Ocean.
| AII-93-5-3/93-3-1/93-8-11:
Age spectra are shown in Figure
5. The plateau ages reported
by O’Connor & Duncan (1990)
are untenable because of very high MSWD values,
corresponding to p values < 10-10
in each case. The isochron plots used by O’Connor
& Duncan (1990) showed MSWD values
of 174, 30 and 2.5 respectively (Baksi,
1999). The first two yield p < 10-10.
For AII-93-8-11, the probability value is 0.08.
However, the isochron is derived from the first
four steps, two of which show very high atmospheric
argon (36Ar) contents. The gas is
derived from altered sites and hence the corresponding
age is suspect (Baksi, 1999). These
three specimens gave no plateau/isochron ages
that can be utilized for tracking hotspot tracks
in the South Atlantic Ocean.
AII-93-10-11:
A plateau age of 46.2 ± 0.3 Ma (Figure
6) was reported by O’Connor
& Duncan (1990). The three-step plateau
yields an acceptable MSWD value (p
~ 0.29). The corresponding isochron (Baksi,
1999) yields a low precision age of 49.8 ±
4.7 Ma, MSWD = 6.2 and p ~ 0.01. This rock could
be said to yield a somewhat imprecise but usable
age for evaluating the hotspot track trace.
Figure
5: Age spectra yielding unacceptable ages from
the Tristan da Cunha hotspot track. |
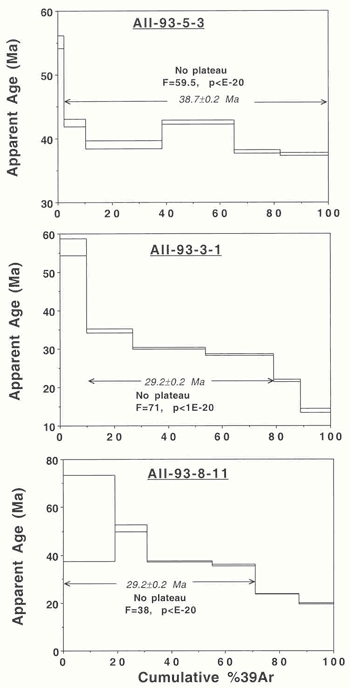
|
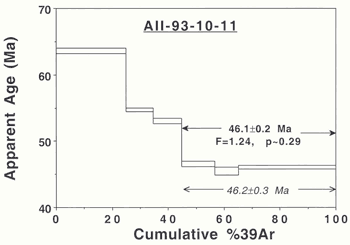
Figure
6: Age spectrum yielding an imprecise but usable
age for evaluating the Tristan da Cunha hotspot
track. |
“Plateau”
ages were also reported by Duncan (1978,
1984) for the track of the Kerguelen Hotspot
in the Indian Ocean and the Great Meteor Hotspot
in the North Atlantic Ocean, respectively. Based
on statistical evaluation of the isochron plots
Baksi (1999) showed that each of these
was untenable. Elsewhere it will be shown that
this conclusion is fully supported by critical
examination of the individual age spectra.
The plate motion model derived
by Muller et al. (1993) was based solely
on the ages referred to above. Only a very few
of these purported ages can be used to date
time of crystallization. The plate motion model
of Muller et al. (1993) is unsubstantiated
since it is not based on a sufficient number
of crystallization ages for hotspot tracks (Baksi,
1999). |
(2) Recent ages for rocks from the British Tertiary
Igneous Province (BTIP).
Chambers & Pringle (2001) reported a
number of plateau/isochron ages for both rocks and
mineral separates from the BTIP. These authors used
these “ages” for defining the time of
initiation and duration of flood-basalt volcanism
in this province and to refine details (cryptochrons)
of the geomagnetic polarity time scale from ~ 60 –
55 Ma. In their Table 1 Chambers & Pringle
(2001) list the MSWD values for their “plateaux”
and isochron plots, and state “of the 10 Mull
samples analyzed, eight met all of the reliability
criteria” (Chambers & Pringle,
2001, p. 334). Critical scrutiny of their data shows
that almost all of their plateau/isochron ages are
unacceptable on statistical grounds. Furthermore,
a cursory glance at the age spectra drawn to an
appropriate scale, shows few if any acceptable
ages were recovered (Figures
7 – 9). I examine their results
for rocks from the Isle of Mull.
SO33, BM67, BM64, B-1:
(All whole-rock samples; see Figure
7). The first (center lava), shows
an age spectrum with numerous ups and downs. Seven
steps were used to arrive at a “plateau”
age of 58.94 ± 0.30 Ma. The corresponding MSWD
value is ~ 19, and p < 10-20.
Clearly this is no plateau. BM67 and 64 (Ben More
lavas) were said to yield plateau ages of 58.66 ±
0.25 Ma and 58.19 ± 0.26 Ma, respectively,
although many step ages obviously do not overlap in
each case. The MSWD ~ 26 and ~ 18, yield p
< 10-20 in each case. Clearly these
ages are unacceptable. Thus what are we to make of
the plateau section for BM64, as defined by Chambers
& Pringle (2001)? Step ages “stagger
around” from ~ 61 – 58 Ma, with each step
error being of the order of 0.20 m.yr. How can one
claim, as do Chambers & Pringle ( 2001),
that the statistically significant mean value is 58.19
± 0.26 Ma? For BI (Lower lava) a descending
age spectrum was used to arrive at a plateau age of
60.56 ± 0.29 Ma. The MSWD value of ~ 15 (p
< 10-14) makes this clearly unacceptable.
The corresponding isochron plots for these four rocks
(Chambers & Pringle, 2001, their Table
1) yield MSWD values of 26, 21, 14 and 11, respectively.
Corresponding p values are < 10-10
in all cases. None of these four rocks yielded a proper
plateau and/or isochron age.
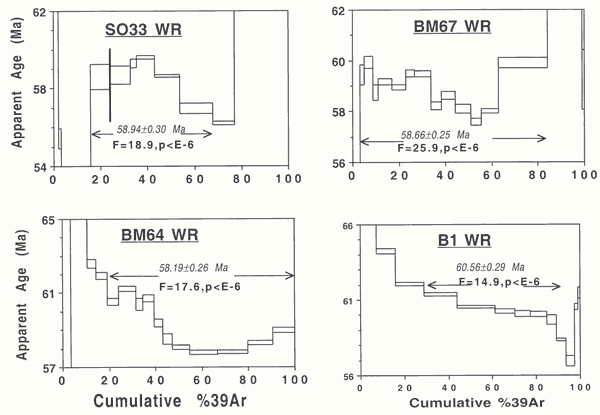
Figure
7: Unacceptable age spectra for samples from the BTIP.
| SO17
(whole-rock – center lava):
The age spectrum (Figure
8) shows that the rock contains
excess argon, giving a saddle-shaped age spectrum
(cf. Lanphere & Dalrymple,
1976). Nine steps define were used by Chambers
& Pringle (2001) to define a plateau
age of 61.54 ± 0.24 Ma. MSWD = 2.02 and
p = 0.04. The corresponding isochron
(Chambers & Pringle, 2001, their
Table 1), shows an initial argon ratio of 316
± 6 (excess argon is present), an age
of 59.66 ± 0.64 and MSWD = 1.28. For
the latter, p = 0.25, making the isochron
but not the plateau age acceptable. Chambers
& Pringle (2001) reject this age on
statistical grounds but accept others with much
worse statistical credentials. |
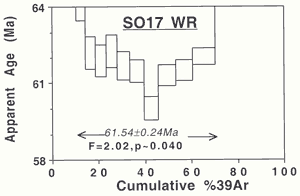
Figure
8: Age spectrum yielding an unacceptable age.
The isochron age for this sample was 59.66
± 0.64 and is acceptable.
|
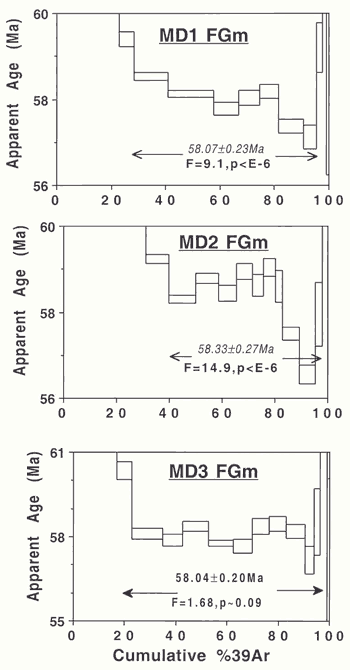
Figure
9: Age spectra that are suggestive of excess
argon. Only sample MD3 (lowermost panel) yields
an acceptable age. |
LB1
(Sanidine – Loch Ba ring dyke): This
mineral has been used very successfully to date
rocks and generally yields good plateau ages.
Chambers & Pringle (2001; their
Figure 2) presented the age spectrum inadequately,
the ordinate running from 40 to 80 Ma (see Figure
2b herein), When replotted for
proper visual inspection (Figure
2d), the age spectrum shows
numerous ups and downs that are much more serious
than the hypothetical case shown in Figure
1. Chambers & Pringle
(2001) used 12 steps to arrive at a “plateau
age” of 58.48 ± 0.18 Ma. Their
MSWD value for these 12 steps is 3.05, for nu
(degrees of freedom = N-1) = 11. The corresponding
Chi Square value is 33.55 (MSWD x nu), and Chi
Square Tables tell us that the probability of
this occurrence is p ~ 0.0004. The age of Chambers
& Pringle (2001) must thus be rejected
on these grounds. The lowest section of the
age spectrum (Figure
2d) shows numerous steps of
~ 58 – 59 Ma. The mineral may
have a crystallization age in this range, but
it contains excess argon (higher step ages on
either side of the “plateau”). There
is no justification for quoting an age of 58.48
Ma with a very small error margin of ±0.18
m.yr. Evaluation of the corresponding isochron
plot gave MSWD = 3.9 (Chambers & Pringle,
2001; their Table 1). This yields p ~ 0.00002. |
Both the plateau
and isochron approach statistics are unequivocal
– a large amount of excess scatter is
present in the data sets (“geological
error”). This mineral separate fails to
yield either a plateau or an isochron age. Note
that almost all the other cases considered in
here yield much lower probability values, often
< 10-6 and in some instances <
10-20! Clearly in such such cases,
the quoted plateau/isochron ages are totally
spurious. |
MD – 1/2/3 (Felsic groundmass separated
from dykes): All three age spectra are
suggestive of the presence of excess argon (Figure
9). Chambers & Pringle
(2001) reported plateau ages of 58.07 ± 0.23
Ma and 58.33 ± 0.27 Ma for MD 1 and 2 respectively.
In both cases MSWD values are very high (~ 10 –
15), with p values correspondingly low (<
10-8 in each case). These ages are rejected.
The corresponding isochron plots also have high MSWD
values (10 and 19), and the associated p
values are extremely low (both < 10-9).
Chambers & Pringle (2001) listed a plateau
age of 58.04 ± 0.20 Ma for MD3. In this instance
the MSWD and p values (1.68 and 0.09 respectively)
are acceptable. The corresponding isochron plot (Chambers
& Pringle, 2001, their Table 1) shows MSWD
= 2.12 (p ~ 0.04) and verges on being acceptable.
The age of this sample can be taken to be 58.1 ±
0.3 Ma.
Summary for Isle of Mull ages
Of the eight specimens said by Chambers
& Pringle (2001) to yield fully acceptable
plateau/isochron ages, on critical examination, only
two pass the relevant statistical tests – SO17
(isochron age) and MD3. The claim that “The duration
of activity that produced the Isle of Mull Tertiary
igneous center has been constrained to 2.52 ±
0.36 million years” (Chambers & Pringle,
2001, p. 333) is thus without scientific basis. These
two acceptable ages, together with one from the Isle
of Skye, do not help to resolve details of the geomagnetic
polarity time scale for the period ~ 61–56 Ma,
and the models shown by Chambers & Pringle
(2001, Figure 5), are without supporting geochronological
data.
Samples from the British Tertiary Igneous
Province have proved more difficult to date accurately
than whole-rock basalts from other flood basalt provinces.
This may be due to the fact that many sections of the
exposed BTIP rocks have undergone low-grade metamorphism
(Mussett, 1986). In my estimation, the best
ages for this province are those of Mussett
(1986) wherein the data were scrupulously evaluated
by proper statistical criteria. These ages are 60.0
± 0.5 Ma for the base of the Mull lava pile and
56.5 ± 1.0 Ma for the Loch Ba dyke (see Chambers
& Pringle, 2001, p. 334).
Concluding Remarks.
All 40Ar/39Ar
age data must be rigorously examined for conformity
to plateau and isochron ages. Figures must be presented
to permit quick but accurate visual inspection of results.
MSWD values must be reported for both plateau and isochron
plots and/or raw data should be included in Tables/Supplementary
Data Sets or made readily available on request. Proper
ages must always be based on at least three consecutive
steps carrying > 50% of the total 39Ar
released. MSWD values for both plateau/isochron data
must yield p values > 0.05 (95% confidence level).
It may be argued that cases with (say) p >
0.01 but < 0.05 should be considered “valid”.
In such cases, where should the line be drawn in
the sand? A 95% confidence test is almost universally
accepted as the first “cut”. Certainly,
ages where the corresponding p values are <
0.001 are anathema.
Good examples of proper statistical
care being exercised in evaluating 40Ar/39Ar
step-heating data, are given, amongst others, in the
work of Mussett (1986) and Knight et al.
(2003). In the absence of proper care being exercised
in these matters by authors/editors/reviewers, it falls
on the reader to evaluate 40Ar/39Ar
ages prior to making use of them. “Always
verify your references” (East, 1998).
Failure to adhere to this adage has led to numerous
incorrect ages becoming entrenched in the literature,
following repeated citation by unsuspecting/uncritical
scientists.
Acknowledgments
I thank Hetu Sheth and especially Gillian Foulger for
making this effort possible. |
-
Baksi, A.K., 1994, Geochronological
studies on whole-rock basalts, Deccan Traps, India:
Evaluation of the timing of volcanism relative to
the K-T boundary, Earth Planet. Sci. Lett.,
121, 43-56.
-
Baksi, A.K., 1999, Reevaluation
of plate motion models based on hotspot tracks in
the Atlantic and Indian Oceans, J. Geol.,
107, 13-26.
-
Baksi, A.K., 2001, The Rajahmundry
Traps, Andhra Pradesh: Evaluation of their petrogenesis
relative to the Deccan Traps, Proc. Indian Acad.
Sci., 110, 397-407.
-
Baksi, A.K., 2003, Critical evaluation
of 40Ar/39Ar
ages from the Central Atlantic Magmatic Province:
Timing, Duration and possible migration of magmatic
centers, in The Central Atlantic Magmatic Province,
Insights from Pangaea, AGU Monograph 136, 77-90.
-
Brooks, C., Hart, S.R., and Wendt,
I., 1972, Realistic use of two-error regression
treatment as applied to rubidium-strontium data,
Rev. Geophys. Space Phys., 10,
551-557.
-
Chambers, L.M. and Pringle, M.S.,
2001, Age and duration of activity at the Isle of
Mull Tertiary igneous center, Scotland, and confirmation
of the existence of subchrons during Anomaly 26r,
Earth Planet. Sci. Lett., 193,
333-345.
-
Dalrymple, G.B., Alexander, E.C.,
Lanphere, M.A., Kraker, G.P., 1981. Irradiation
of samples for 40Ar/39Ar
dating using the Geological Survey TRIGA
Reactor, U.S. Geol. Surv. Prof. Paper 1176,
55 pp.
- Dalrymple, G.B., M.A. Lanphere and M.S. Pringle,
Correlation diagrams in Ar-40/Ar-39 dating - Is there
a correct choice?, Geophys. Res. Lett., 15,
589-591, 1988.
-
DeVor, R.E., Chang, T-H., Sutherland,
J.W., 1992, Statistical quality design and control,
Prentice-Hall, Upper Saddle River, New Jersey, pp.
787-797.
-
Duncan, R.A., 1978, Geochronology
of basalts from the Ninetyeast Ridge and continental
dispersion in the eastern Indian Ocean, J. Volcanol.
Geotherm. Res., 4, 283-305.
-
Duncan, R.A., 1984, Age progressive
volcanism in the New England Seamounts and the opening
of the central Atlantic Ocean, J. Geophys. Res.,
89, 9980-9990.
-
East, A.L., 1998, The finer points
of mythology and science, Eos, Trans. AGU,
79, 402.
-
Knight, K.B., Renne, P.R., Halkett,
A.,White, N., 2003, 40Ar/39Ar
dating of the Rajahmundry Traps, Eastern
India and their relationship to the Deccan Traps,
Earth Planet. Sci. Lett., 208,
85-99.
-
Lanphere, M.A., Dalrymple, G.B.,
1976, Identification of excess 40Ar
by the 40Ar/39Ar
age spectrum technique, Earth Planet.
Sci. Lett., 32, 141-148.
-
Lanphere, M.A., Dalrymple, G.B.,
1978, The use of 40Ar/39Ar
data in evaluation of disturbed K-Ar systems,
U.S. Geol. Surv. Open-File Rpt. 78-701,
241-243.
-
Muller, R.D., Royer, J-Y., Lawver,
L.A., 1993. Revised plate motions relative to hotspots
from combined Atlantic and Indian hotspot tracks,
Geology, 21, 275-278.
-
Mussett, A.E., 1986, 40Ar-39Ar
step-heating ages of the Tertiary igneous
rocks of Mull, Scotland, J. Geol. Soc. London,
143, 887-896.
-
O’Connor, J.M., Duncan,
R.A., 1990. Evolution of the Walvis-Rio Grande Rise
hotspot system: implications for African and South
American motions over plumes, J. Geophys. Res.,
95, 17,475-17,502.
-
Roddick, J.C., 1978, The application
of isochron diagrams in 40Ar-39Ar
dating: a discussion, Earth Planet. Sci.
Lett., 48, 185-208.
-
York, D., 1969, Least squares
fitting of a straight line with correlated errors,
Earth Planet. Sci. Lett., 5,
320-324.
last updated April 2nd, 2006 |
|
|
