 |
An alternative mechanism of formation of continental flood basalts: The volcanic systems approach |
Edgardo Cañón-Tapia
CICESE, Depto. de Geología, Carretera Ensenada-Tijuana No. 3918, Fraccionamiento Zona Playitas, Ensenada, Baja California, C.P. 22860, ecanon@cicese.mx
This webpage is a summary of: Cañón-Tapia, E., 2010, Origin of Large
Igneous Provinces: The importance of a definition,
in Cañón-Tapia, E., and Szakács,
A., eds., What Is a Volcano?: Geological Society
of America Special Paper 470, p. 77–101,
doi: 10.1130/2010.2470(06).
The definition of a large igneous province (LIP) advanced by Coffin & Eldhom (1992) implies that such provinces should be created by mechanisms entirely different from those operating in the formation of other volcanic provinces on Earth. The extraordinary character of LIPs, as part of that definition, also has been invoked in essentially all current explanations for their genesis. In particular, it has become common place to visualize LIPs as the result of extraordinary rapid production of magma that is not observed in non-LIPs around the globe. Nevertheless, the extraordinary character of LIPs is not a valid concept insofar as magma production rates cannot be measured directly at either ancient or modern volcanic provinces. The only directly quantifiable parameter in any volcanic province related to magma production rate is extrusion rate. Thus, to understand better the genesis of LIPs, it is important to clarify the relation between magma production rate, extrusion rate, and volumes stored at a given time in a region of partial melting (RPM).
This can be done schematically by assuming a constant magma production rate at all times. In Figure 1, the discontinuous line drawn from t0 to t6 represents the volume of magma stored at depth in the absence of extrusion events. If periods of melt tapping are allowed to occur, while keeping magma production constant, the amount of melt available at any time in the RPM will instead be indicated by the solid line with different slopes. The changes in the slope of the solid line in the intervals t1-t2, t3-t4, and t5-t6 are associated with the tapping events E1 to E3, displayed at the lower end of the diagram. The rate at which magma is tapped from the RPM is equal to (E1), smaller than (E2) and larger than (E3) the rate of magma production.
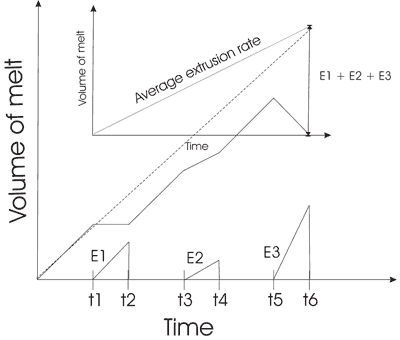
Figure 1: Relationship between magma production rate, volume of magma stored in a RPM, and magma tapping events.
Although schematic, Figure 1 illustrates several important aspects concerning the dangers of estimating magma production rate using data that strictly belong to magma extrusion rates.
-
A variety of extrusion rates can be supported by a single value of magma production rate.
-
Extrusion rates faster than production rates are sustainable only if there is a delay between the moment of initiation of magma production and the initiation of the extrusive event. The longer this delay, the longer the time a high extrusion rate can be sustained before exhausting the melt available.
-
Although the cumulative extruded volumes can be used to calculate an average magma production rate (light axes at the top of the figure), the slope of this curve does not necessarily represent the actual magma production rate because we ignore the exact moment when magma began to be produced (i.e., t0 is not equal to t1).
-
The total volume existing at depth a given time cannot be determined from the volume of erupted products.
-
Even very slow production rates may sustain high rates of extrusion given adequate time for magma accumulation.
-
If we disregard the extrusive events, the solid line would seem to include changes in magma production rate at t1, t2, t3, etc. because these points mark a shift in the slope of the melt volume as a function of time. This interpretation would be at odds with the constant magma production rate assumed originally.
The extraordinary character of LIPs is shared by a subgroup of volcanic provinces known as Continental Flood Basalts (CFBs). It is easier to obtain reliable quantitative information from CFBs than for other LIPs. Consequently, it is advantageous to focus on CFBs for some purposes.
Radiometric ages of CFBs indicate that peak extrusion rates might have exceeded 100 km3/yr, although rates are more commonly in the range 0.5 to a few tens of km3/yr (Coffin & Eldhom, 1994). In contrast, when proper attention is given to the various sources of potential errors, extrusion rates in modern volcanic provinces are in the range 0.01-1 km3/yr (Harris et al., 2007).
If the high end of extrusion rates of CFBs is compared to the lower end in modern volcanic provinces, the difference between the two kinds of volcanic activity is strikingly large. If attention is focused on the other extremes of both ranges, however, it turns out that not only is the difference between the two small, but even that at least in some cases the extrusion rates in modern volcanic provinces might have been actually higher than in CFBs (Figure 2).
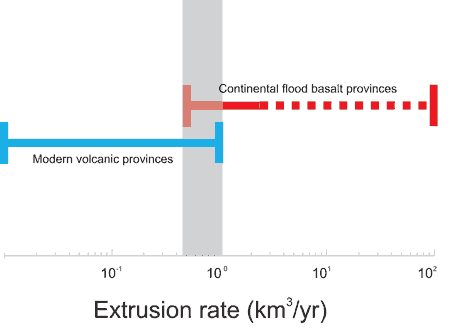
Figure 2: Comparison between magma extrusion rates characteristic of modern volcanic provinces and CFBs. The shadowed area shows the overlap.
Based on seismic observations beneath zones of active volcanism, the zones of low velocity likely to contain melt can be defined as having lateral extensions of 200 km or even larger, and thicknesses of the order of 50-100 km (Nakajima et al., 2005; Panza et al., 2003; Ryan, 1990; Watson & McKenzie, 1991). If we consider that melt proportions can be 2-15% (e.g., Sato & Ryan, 1994) we can conclude that typical volumes of present-day RPMs are of the order of 106 km3. Even larger dimensions could be obtained for low-velocity zones beneath tectonically active regions (e.g., Grand, 1994).
Unfortunately, seismic methods cannot be used to constrain the volume of melt stored beneath any LIP or CFB during its formation. Consequently, we must look for an alternative source of information that allows us to constrain such a variable. Ideally, and in order to avoid the fallacy of four terms (Copi & Cohen, 1994), we need to estimate magma volumes in both CFBs and modern volcanic provinces using the same method. This can be achieved by measuring the content of rare earth elements (REE) in the volcanic products (White & McKenzie, 1995). Leaving aside the influence of choice of mantle source, melting process and transport mechanisms, a key aspect of this method is that it can be used with the same premises to constrain melt distribution beneath volcanic provinces, young or old (Figure 3). Consequently, the results can be compared directly without falling into a fallacious argument.
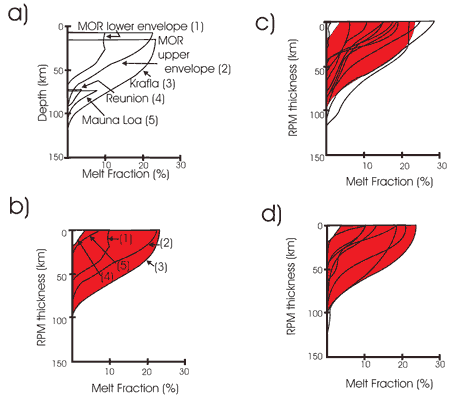
Figure 3: Melt distributions with depth inferred from rare earth element inversions (White & McKenzie, 1995). a) Curves from basalts from Mid Ocean Ridges and intraplate volcanoes. For MORBs only the upper and lower limits of the melt distributions are shown. The same curves of diagram (a) are shown in (b) with their upper limit displaced to emphase the dimensions of various regions rather than the depths at which they are generated. The shadowed area is an envelope used for comparative purposes in (c) and (d). c) Comparison of the melt distributions of b) with those inferred from the Siberian traps, Keweenawan, the North Atlantic, the Columbia river, Deccan, Etendeka, Parana, Karoo and Coppermine River (examples from White & McKenzie, 1995). d) Comparison of the melt distributions of diagram b) with those inferred from various basalt and dykes ranging in age from 0 – 2700 Ma.
Although according to this method magmas produced in MORs tend to be formed at shallower depths than intraplate magmas (Figure 3a), the same data also reveal that the inferred melt distributions define a layer some 100 km thick regardless of tectonic setting (Figure 3b). Such melt distribution curves imply that average melt fractions (estimated as the areas to the left of the inferred melt distribution curves normalized by the thickness of the corresponding RPM) are also relatively constant (~ 5-15%) irrespective of the tectonic scenario. This is in agreement with the information inferred from seismic methods on those provinces. Notably, from the nearly 30 CFB-related melt distributions examined by White & McKenzie (1995), of which only a representative selection was included in Figure 3c for clarity, neither the associated thickness of the RPM nor the average melt content are unusually larger than the upper limits of present-day volcanically active provinces. Furthermore, it is possible to identify particular examples in which the CFB melt distribution is smaller than the lower limit of modern volcanic provinces. If lavas and dykes ranging in age from 0 to 2700 Ma are also considered, the same basic result is obtained (Figure 3d).
Although the REE method suggests that the percentage of melt might change drastically with depth, a conservative estimate of the typical melt content of the RPMs feeding all types of volcanic provinces can be considered to be 5% throughout a layer 100 km thick. A simple calculation based on the constraints shown in Figure 4 indicates that RPMs beneath present-day active volcanic provinces conservatively might contain ~105 km3 of melt. Therefore, the volume of melt beneath volcanic regions might be much larger than the volume extruded in any single eruptive event either in modern volcanic provinces or CFBs.
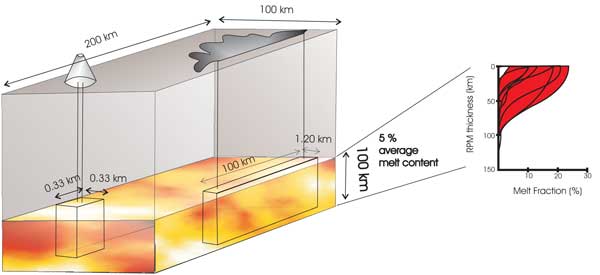
Figure 4: Schematic relation of the volumes of mantle required to produce the erupted volumes in one eruption of a normal volcano (cone) and a CFB-forming event (elongated feature on the surface). The average melt content of the melt zone is consistent with the constraints imposed by melt distributions inferred from rare earth compositions of erupted products (Figure 4) and reproduced in the right of the diagram. The dimensions of the regional LVZ are shown on the upper part of the box. Click here or on figure for enlargement.
Considering that a typical eruption in a modern volcanic province extrudes ~ 0.5 km3 of magma, whereas that of a single extrusion event in a CFB might reach 600 km3, it follows that a typical present-day RPM conservatively can supply over 300 eruptive events of CFB proportions. Remarkably, the number of eruptions that could be supplied from already existing magma in present-day RPMs would account for nearly 20% of the total volume of extrusive products characteristic of CFB provinces without requiring the production of a single additional drop of melt. If the calculations were made using the limit of 15% melt (well within the limits allowed by observations), the volume of melt potentially existing in many RPMs could account for 60% of the volume of a typical LIP. Thus, it is clear that present-day volumes of magma trapped at depth have the potential to build LIP-sized volcanic provinces. Furthermore, if normal magma production rates replace the melt extracted, it may be concluded that, at least in theory, CFBs (and LIPs by extension) are not the result of extraordinary magma production events, but constitute the high end of a continuum of normal processes within Earth.
If a typical, present-day RPM has the potential to feed an eruptive event as volumetrically impressive as any in a CFB province, we need to explain:
- why all the melt is not currently being extruded, and
- what is responsible for the occasional efficient melt extraction event.
A clue to answer both questions can be found by focusing on key aspects controlling the processes of melt extraction from its source and transport to the surface as described in the general model of volcanism advanced by Cañón-Tapia & Walker (2004).
The first step is to constrain the minimum amounts of magma required to initiate a tapping event. It can be shown that in general critical heights of <100 km will suffice to initiate hydraulic fracturing under most geologically relevant conditions (Cañón-Tapia, 2008; 2009). The exact critical height depends on the depth at which the base of the RPM is located, but it is entirely independent of the volume of magma involved. For example, 1 km3 of magma would suffice to initiate a tapping event if it were all in a narrow conduit with a horizontal surface area of ~0.02 km2 and a vertical extent of 50 km. In contrast, even 10 km3 of magma would not suffice to initiate a tapping event if it were contained in a large pool with a horizontal area of ~10 km2 and a depth of only 1 km (Figure 5). The difference between these two cases is that in the former the column of magma creates vertical excess stress sufficient to induce horizontal tensional stress slightly larger than the tensile strengths of most rock (red vertical lines in Figure 6). In contrast, the larger volume pool of magma only results in a vertical excess stress of >10 MPa under most conditions of geological interest, which would induce a tensional horizontal stress <3 MPa in most cases (blue vertical lines in Figure 6). Consequently, whereas the minimum volume of magma required to initiate magma tapping can be constrained using hydrostatic principles, there are no constraints that can be imposed on the maximum volumes involved in any tapping event other than perhaps specifying a maximum melt fraction for a given volume of mantle rock.

Figure 5: A relatively small volume of magma (red) can result in a tapping event if its vertical dimension is large enough, whereas a relatively large volume (blue) will not be extracted from the RPM if its vertical dimension is small. The hydraulic head associated to each of the volumes in this figure also depends on the depth at which its base is located, and on the exact density contrast with the country rock. Nevertheless, as shown by the corresponding lines in Figure 6, the smaller volume has a much larger hydraulic head than the larger volume in all circumstances.
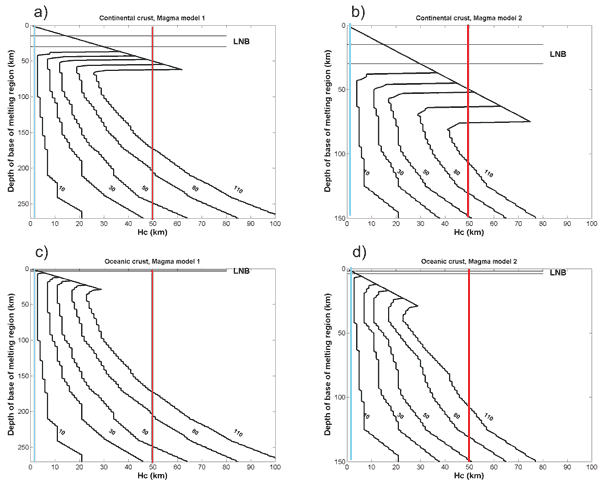
Figure 6: The size of the critical heights of a column of magma required to exert a vertical stress of the size shown numerically by each curve, as a function of the depth of the base of the column. The two magma models correspond to densities of melt calculated from the two cases of Stolper et al. (1981), each applied considering a column of solid rock having either oceanic or continental crust above the melt [from Cañón-Tapia, 2008]. Click here or on figure for enlargement.
For the two situations I shall consider next it can be assumed that a RPM has lateral dimensions of 100 km x 100 km, and a thickness of 50 km, containing an average 1% melt (Figure 4). From the total 500 km3 of melt contained in the RPMs of each of the two examples, I will assume only 120 km3 of liquid for simplicity, but note that the same calculations can be done by using any other prescribed volume without altering the main conclusions.
In one case, the 120 km3 of melt are concentrated in two zones, each 20 km x 1.2 km in the horizontal and 50 km in the vertical direction. In the other case the RPM has the same 120 km3 of magma dispersed in 445 parcels of rock, each having horizontal dimensions of 0.33 x 0.33 km and with a vertical extent of 50 km. In both RPMs the remaining 380 km3 of magma are uniformly distributed throughout the remaining 47,600 km3 of mantle rock defining the RPM. In other words, although the average melt content of each RPM is equal to 1%, the melt is concentrated in regions having 5% melt concentration and regions having 0.8% melt, and those regions of higher melt concentration are distributed differently in each.
Since the volume of magma tapped by any propagating fracture will be limited to the melt contained by the region immediately around the first fracture, when the zones of melt concentration are small the volume of melt involved is of the order of 0.27 km3. This corresponds to the volume of magma erupted in a modern volcanic province. Even if the fracture extended beyond the horizontal limits of one region of high melt concentration, the lateral extent of this fracture would add only small volumes of melt because it would pierce the surface of a volume of mantle with very small amounts of magma. Because the mechanism driving the propagation of the fracture front both in the horizontal and the vertical directions depends on the volume of melt entering the newly formed crack (Cañón-Tapia & Merle, 2006), it is unlikely that a single fracture could propagate long enough along the surface of the RPM to intersect a second region of high melt concentration. Consequently, any tapping event in the RPM is likely to involve very small volumes of magma at one time.
In contrast, any fracture that nucleates where zones of melt concentration are large, tapping magma is likely to involve up to 60 km3 of liquid in a single event. The tapping of such volume could occur through a conduit of relatively limited horizontal extension, provided that the horizontal interconectivity is sustained in the zone of melt concentration. Alternatively, it might involve a fracture with a horizontal extension of a few kilometers in one direction if the fracture allowing mobilization of magma grows along the top of the RPM parallel to the longest horizontal dimension of the zone of melt concentration. In either case, a volume of liquid corresponding to one volcanic eruption of a CFB province will be tapped in a single event with relatively ease.
Despite the fact that both examples shown in Figure 4 are simplified, they illustrate that, at least in theory, two contrasting eruptive behaviors can originate from RPMs containing identical melt fractions and total amounts of magma. Variations in the internal distribution of melt, rather than actual melt content, can explain different eruptive behaviors seen in CFBs and modern volcanic provinces. In addition, these examples suggest that variations in the internal distribution of melt in a RPM can also explain why a present-day RPM might not feed a CFB. It may also give clues concerning the processes that could lead to the conditions required for the creation of a CFB from time to time.
Several processes could lead:
- to the uneven accumulation of melt within a RPM, and
- to favor the rupture of the upper boundary of the RPM for long horizontal distances.
One possible alternative to satisfy both conditions is the action of mantle plumes. This explanation, however, is not unique and other geologically plausible scenarios need to be explored. A reasonable scenario arises from the observed coincidence between CFBs and lithospheric discontinuities such as craton boundaries or ancient shear zones (Anderson, 1994). King & Anderson (1995) showed that a large change in lithosphere thickness can induce small scale mantle convection capable of producing a RPM with zones of melt concentration exceeding 2%. According to their results, the more marked the difference in lithospheric thickness the more extensive the zones of melt accumulation and consequently the larger the volume of melt that could be stored. Furthermore, their model shows that a regional zone of partial melt would not have an homogeneous distribution, but rather melt will tend to concentrate in two or three broad zones (depending on the difference in lithospheric thickness) separated by zones with lower concentrations of melt. Although those results represent idealized situations, an extensive zone of partial melt with some zones of higher melt concentration separated by zones of lower melt concentration is one of the conditions required by the model developed above.
The same mantle geometry explored by King & Anderson (1995) favors the rupture of the RPM for long distances. Analogue models of overpressured magma chambers with different geometries (Cañón-Tapia & Merle, 2006) show that rupture events are more likely to nucleate in those places on the surface of the chamber having a larger angularity, and that such angularities guide the propagation of the fracture along the surface of the chamber once it had started to form. Thus, the angularities associated with the step in lithospheric thickness could serve as nucleation sites for fractures that allow the rapid tapping of magma formed in small convection cells. Finally, the vertical dimensions of the zones of higher melt concentration in the numerical results of King & Anderson (1995) are within the limits of the 100 km required to initiate a tapping event based solely on the difference in density of the magma with its surroundings. Consequently, in contrast to the conclusions of King & Anderson (1995), a mechanism for the melt to reach the surface does exist even without an external source of lithospheric extension. If such extension occurred as the result of other, larger scale processes, the initiation of the fracturing event will be further facilitated, and could be achieved by columns of magma of less than 50 km high.
CFBs and modern volcanic provinces result from the same basic processes. The most striking difference between them, the large difference in typical erupted volumes, can be explained by conditions that are not extraordinary or anomalous. For this reason, it is concluded here that CFB provinces, and by extension LIPs, are not necessarily the manifestations of a significantly different mode of behavior of the Earth, but rather one extreme of a spectrum of possible outcomes that can occur as a result of variations in the various parameters that control volcanic activity. Relatively small variations in some of these are likely to be responsible for the wide diversity of features displayed by LIPs and modern volcanic provinces alike, including those related to chemical composition.
The ideas presented in this webpage are summarised from the paper by Cañón-Tapia (2010), where more details can be found, including related philosophical arguments.
References
-
Anderson, D., L., 1994. Superplumes or supercontinents? Geology, 22: 39 - 42.
-
Cañón-Tapia, E., 2010, Origin of Large
Igneous Provinces: The importance of a definition,
in Cañón-Tapia, E., and Szakács,
A., eds., What Is a Volcano?: Geological Society
of America Special Paper 470, p. 77–101,
doi: 10.1130/2010.2470(06)
-
Cañón-Tapia, E., 2009. Hydrostatic principles of volcanic systems. In: T. Thordarson, G. Larsen, S. Self, S. Rowland and A. Hoskuldsson (Editors), Studies in volcanology: The Legacy of George Walker. The Geological Society, London, pp. 267 - 289.
-
Cañón-Tapia, E., 2008. How deep can be a dyke? Journal of Volcanology and Geothermal Research, 171: 215 - 228.
-
Cañón-Tapia, E. and Merle, O., 2006. Dyke nucleation and earlier growth from pressurized magma chambers: Insights from analogue models. Journal of Volcanology and Geothermal Research, 158: 207 - 220.
-
Cañón-Tapia, E. and Walker, G., P., L., 2004. Global aspects of volcanism: the perspectives of "plate tectonics" and "volcanic systems". Earth Science Reviews, 66: 163 - 182.
-
Coffin, M., F. and Eldholm, O., 1992. Volcanism and continental break-up: a global compilation of large igneous provinces. In: B. Storey, C., T. Alabaster and R. Pankhurst, J. (Editors), Magmatism and the causes of continental break-up. The Geological Society, London, pp. 17 - 30.
-
Coffin, M., F. and Eldhom, O., 1994. Large igneous provinces: Crustal structure, dimensions, and external consequences. Reviews of Geophysics, 32: 1 - 36.
-
Copi, I., M. and Cohen, C., 1994. Introduction to logic. Macmillan Publishing Company, New York, 729 pp.
-
Grand, S., P., 1994. Mantle shear structure beneath the Americas and surrounding oceans. Journal of Geophysical Research, 99: 11 591 - 11 621.
-
Harris, A., J., L., Dehn, J. and Calvari, S., 2007. Lava effusion rate definition and measurement: a review. Bulletin of Volcanology, 70: 1 - 22.
-
King, S., D. and Anderson, D., L., 1995. An alternative mechanism of flood basalt formation. Earth and Planetary Science Letters, 136: 269 - 279.
-
Nakajima, J., Takei, Y. and Hasegawa, A., 2005. Quantitative analysis of the inclined low-velocity zone in the mantle wedge of northeastern Japan: a systematic change of melt-filled pore shapes with depth and its implications for melt migration. Earth and Planetary Science Letters, 234: 59 - 70.
-
Panza, G., F., Pontevivo, A., Chimera, G., Raykova, R. and Aoudia, A., 2003. The lithosphere-astenosphere: Italy and surroundings. Episodes, 26: 169 - 174.
-
Ryan, M., P., 1990. The physical nature of the Icelandic magma transport system. In: M. Ryan, P. (Editor), Magma transport and storage. John Wiley & sons, Chichester, pp. 175 - 224.
-
Sato, H. and Ryan, M., P., 1994. Generalized upper mantle thermal structure of the western United States and its relationship to seismic attenuation, heat flow, partial melt and magma ascent and emplacement. In: M. Ryan, P. (Editor), Magmatic systems. International geophysics series. Academic Press, San Diego, pp. 259 - 290.
-
Stolper, E., Walker, D., Hager, B., H. and Hays, J., F., 1981. Melt segregation from partially molten source regions: the importance of melt density and source region size. Journal of Geophysical Research, 86: 6 261 - 6 271.
-
Watson, S. and McKenzie, D., 1991. Melt generation by plumes: A study of Hawaiian volcanism. Journal of Petrology, 32: 501 - 537.
-
White, R., S. and McKenzie, D., 1995. Mantle plumes and flood basalts. Journal of Geophysical Research, 100: 17 543 - 17 585.
last updated 1st June, 2012 |
