Deep and near-surface consequences of root removal by asymmetric continental delamination

J.L. Valera¹, A.M. Negredo^1,2 and I. Jiménez-Munt³

¹Departamento de Física de la Tierra, Astronomía y Astrofísica-I, Facultad de CC. Físicas, Plaza de Ciencias 1. 28040-Madrid, Spain, jlvalera@fis.ucm.es anegredo@fis.ucm.es

²Instituto de Geociencias (CSIC-UCM), Facultad de CC. Físicas, Plaza de Ciencias 1. 28040-Madrid, Spain, anegredo@fis.ucm.es

³Instituto de Ciencias de la Tierra ‘Jaume Almera’. CSIC. C/ Sole i Sabaris s/n. 08028 Barcelona. Spain, ivone@ictja.csic.es

This webpage is a summary of the paper: Valera, J.L., A.M. Negredo, I. Jiménez-Munt, Deep and near-surface consequences of root removal by asymmetric continental delamination, Tectonophysics, 502, 257-265, 2011.

Continental delamination is a mechanism commonly invoked in many areas to explain removal of continental lithospheric mantle. Delamination is different from convective removal processes, and very few physical-numerical models have been developed (e.g. Scott & Schmeling, 1998; Morency & Doin, 2004; Gögüs & Pysklywec, 2008). As a result, basic aspects of this process remain poorly understood. Moreover, the consequences of the delamination mechanism on the evolution of surface and near-surface observables, namely the crustal structure, topographic response (both isostatic and dynamic) and surface heat flow, are still under debate. We present results of numerical simulations considering different initial setups, representative for different geodynamic scenarios prone to delamination, focusing on the evolution of the previously mentioned observables. We used the thermo-mechanical numerical algorithm TEMESCH developed by Valera et al. (2008) in MATLAB code (Negredo et al., 2004; Valera et al. 2008).

Figure 1 presents the evolution of our Reference Model. It has an orogenic lower crust with a density of 3050 kg/m³, and mimicks a post-collisional orogenic scenario. The leftwards migration of the delaminated slab pulls the thickened crust and produces crust/lithosphere thickening in front of the migrating delamination point and crust/lithosphere thinning behind it. The space vacated by the migrating lithospheric mantle is filled up by the ascent of asthenospheric mantle up to the Moho. This coupled crustal thickening/thinning is also obtained in the modeling of Schott & Schmeling (1998) and by Gögüs & Pysklywec (2008) and can therefore be considered to be a characteristic feature of the delamination mechanism. Lower crustal material is pulled down by viscous drag of the delaminated lithospheric mantle, and the Moho reaches depths of about 100-130 km at around 15 Ma. The dragged-down crust forms a thin, vertically elongated layer over the sinking lithospheric material, similar to the typical shape adopted by crust in an oceanic subduction zone.

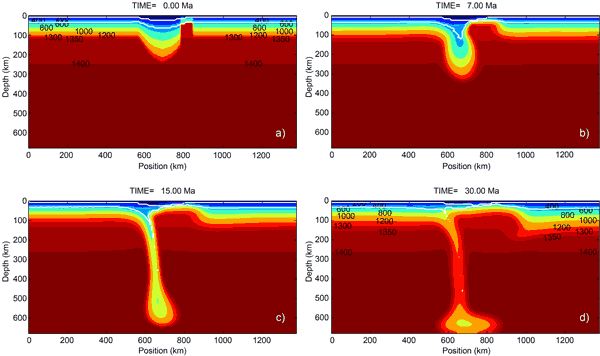
Figure 1: Evolution of the Reference Model for the delamination process. Colors represent temperature distribution with labels in ºC; white lines show the bases of the upper and lower crust. Click here or on figure for enlargement.

Figure 2 shows a comparison after 15 Ma of the evolution of the Reference Model (Figure 2a-c) and another model with a less-dense lower crust (Figure 2d-f). It is remarkable that by reducing only the density of the orogenic lower crust the delamination process is significantly slowed down. We can therefore infer that, at least for this orogenic crust initial configuration, the density of the orogenic lower crust strongly affects the development of delamination, although the patterns of predicted surface heat flow and topography are similar for both models. The predicted local isostatic topography shows a leftwards migrating pattern of uplift/subsidence, following the leftwards migration of delaminating lithospheric mantle and of crustal thickening over the slab.

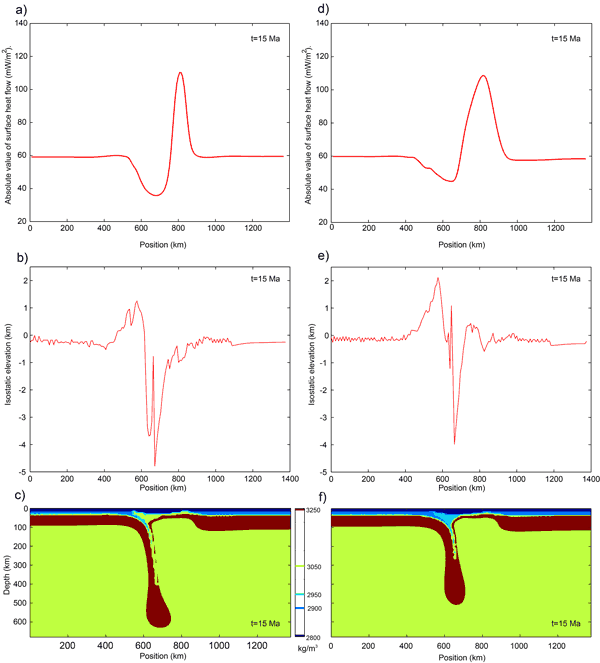
Figure 2: Comparison after 15 Ma of evolution of the Reference Model (a-c) and a model with a less dense lower crust of 2950 kg/m³ (d-f). The compared observables are the surface heat flow (a, d), the local isostatic topography (b, e) and the density distribution (c, f) showing only a series of discrete values for density. Click here or on figure for enlargement.

Figure 3 shows predicted dynamic topography after 15 Ma of evolution of two models with exactly the same configuration and density as shown in Figure 2, but introducing a ‘soft sediments’ upper layer in order to allow for the top of the crust to behave as a free surface. In these models, delamination develops slightly slower than in models without this layer because isotherms are shifted upwards to include this new layer. Therefore the lithosphere is initially hotter and slightly more buoyant than in models without a ‘soft sediment’ layer. The predicted dynamic topography shows surface subsidence adjacent to the delaminating lithospheric mantle for the model with a high-density orogenic lower crust (Figure 3a), and surface uplift above the slab for a model with a lighter orogenic lower crust (Figure 3c). The uplift in this second model is explained by the effect of the positive buoyancy of the thickened crust, which overcomes the effect of negative buoyancy of the delaminated lithospheric mantle. We therefore show that the density of the lower crust also has a significant influence on the dynamic topography response related to delamination.

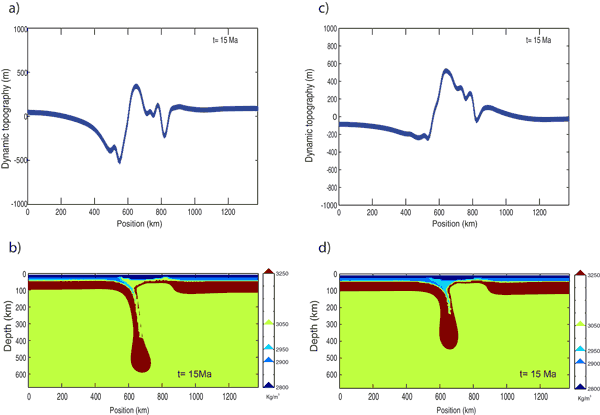
Figure 3: Predicted dynamic topography (a, c) and density distribution (b, d) after 15 Ma of evolution of two models with ‘soft sediments’ upper layer. The model displayed to the left (a, b) has and orogenic lower-crust density of 3050 kg/m³ (same value as the Reference Model) and the model displayed to the right (c, d) has an orogenic lower-crust density of 2950 kg/m³. Click here or on figure for enlargement.

To mimic the evolution of a post slab break-off scenario, we perform a model with an initial setup consisting of a flat crust with a standard value of lower crust density (2950 kg/m³) and including a region of thickened lithospheric mantle (to mimic a remnant portion of slab). The evolution is similar to previous model (compare Figure 4 a-b with Figure 2e-f and Figure 4c-d with Figure 3c-d), but evolves faster because the area occupied by the crustal root in previous models is now occupied by denser lithospheric mantle. The evolution predicted with this model highlights that, provided there is sufficient negative buoyancy, a thickened low-viscosity layer (represented by the lower crust) is not needed to obtain delamination. We obtain the same pattern of crustal thickening/thinning associated with the migrating delamination point. In contrast, the topographic response is very different (Figure 4), as uplift is not predicted in any part of the modeled section. The high negative predicted isostatic topography (Figure 4a) results from the strong mass excess in the lithospheric mantle imposed in this model. Similarly, the equivalent model including a layer of ‘soft sediments’ also predicts surface subsidence for the same area above the delaminated lithospheric mantle (Figure 4c-d).

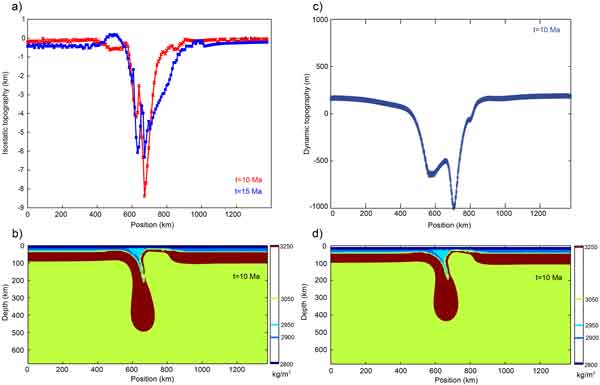
Figure 4: Model-predicted local isostatic topography (a) after 10 and 15 Ma of evolution, and density distribution after 10 Ma (b) for a model with a flat geometry of the crust. Predicted dynamic topography (c) and density distribution (d) after 10 Ma of evolution for a model with the same configuration but including a ‘soft sediments’ upper layer. Click here or on figure for enlargement.

According to the models presented here, there is no specific characteristic pattern of topography changes associated with delamination, but changes result from the interplay between highly variable factors, such as slab sinking velocity, asthenospheric upwelling and changes in crustal thickness. Therefore, caution must be taken when possible delamination processes are inferred only on the basis of topographic evolution.

References

• Gögüs, O.H, Pysklywec, R.N. (2008), Near-surface diagnostics of dripping or delaminating lithosphere, Journal of Geophysical Research, 113, B11404, doi:10.1029/2007JB005123
• Morency, C.Y., Doin, M.-P. (2004), Numerical simulations of the mantle lithosphere delamination. Journal of Geophysical Research, 109, B03410, doi: 10.1029/2003JB002414.
• Negredo, A.M., Valera, J.L., Carminati, E. (2004), TEMSPOL: a MATLAB termal model for deep subduction zones including major phase transformations. Computers & Geosciences, 30, 249–258
• Schott, B.Y., Schmeling, H. (1998), Delamination and detachment of a lithospheric root. Tectonophysics, 296, 225-247.
• Valera, J.L., Negredo, A.M., Villaseñor, A. (2008), Asymmetric delamination and convective removal numerical modeling: Comparison with evolutionary models for the Alboran Sea region, Pure and Applied Geophysics, 165, 1683–1706, doi:10.1007/s00024-008-0395-8