EDGE-driven convection

Introduction

Edge Driven Convection (EDC) is an instability that occurs at the boundary between thick stable lithosphere (for example, an Archean craton) and thinner lithosphere (King & Anderson, 1998; King & Ritsema, 2000). Elder (1976) first discussed the effect of flow near a stationary continent drawing on the results of laboratory experiments. Vogt (1991) proposed that a pair of asthenospheric upwellings, paralleling and controlled by the temperature contrast across the North American continental margin were responsible for formation of the Bermuda and Labrador rises. King & Ritsema (2000) present images from a seismic tomography model that are consistent with the down-welling limbs of the EDC instability associated with cratonic roots under Africa. These examples appeal to a small-scale instability driven by lateral variations in temperature near the top of the mantle (Anderson, 2001).

The vertical cross section through the tomographic model S20RTS (Ritsema et al., 1999) across the south-central Atlantic has been interpreted by King & Ritsema (2000) as downwelling limbs under the Atlantic side of the African and South American cratons (Figure 1). The saturated blue region in the upper 100 km is 4% faster than PREM while the blue limbs, which extend to 500 km depth, are interpreted as the down-going limbs of the EDC instability. Because of ray focusing and dispersion, it may be easier to image the cold, fast, down-going limbs of the EDC flow than the warmer, upwelling part of the EDC flow that we expect to find beneath hotspots. A corollary of this is that seismic experiments testing the EDC flow hypothesis should have a distribution of stations covering not only the hotspot under investigation, but also the potential “edge”.

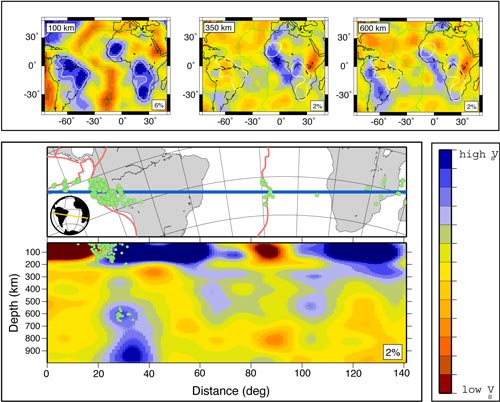
Figure 1: A vertical cross-section through the tomographic model S20RTS. Velocity anomalies are referenced to PREM. Blue regions represent anomalies larger (faster) than PREM and red represent regions smaller (slower) than PREM. The scale is ± 2%. (Adapted from King & Ritsema, 2000).

EDC requires a stable, thick continental or cratonic root adjacent to a thinner (probably oceanic) plate. Because of our limited knowledge of the thermal, mechanical and chemical properties of the cratonic root, it is difficult to place a bound on the minimum thickness root necessary to generate an EDC instability. While not exhausting parameter space, our numerical experiments suggest that a 150 km thick craton/root is the minimum required.

Seismic evidence supports the existence of such roots under thick cratons (e.g., Sipkin & Jordan, 1975; Ritsema et al., 1999). The lack of correlation between the long-wavelength geoid and continents (Kaula, 1967; Shapiro et al., 1999a) indicates that continental roots are not simply structures formed by prolonged conductive cooling and must be compositionally distinct from the upper mantle. The long-term stability of these roots is assumed in the EDC hypothesis; however EDC is not related to the “delamination” of the continental root. The stability of thermo-chemical continental roots is a different problem that has been examined by Shapiro et al. (1999b).

EDC is driven by the vertical temperature variation along the “edge” (boundary) of the cratonic root. Because the craton and the cratonic root are assumed to have been stable for a billion years or more, we assume that the root is not significantly deforming and that from the point of view of the mantle, this root is a stable, fixed boundary. This is not to say that there is not a small amount of erosion of the cratonic root during this process, but including this effect is computationally challenging and introduces a new set of issues to be considered including the strength and composition of the cratonic root. Therefore we begin with the fairly simple assumption that the cratonic root is a rigid and undeforming boundary. Because the craton and oceanic lithosphere are stable, fixed boundaries and the mantle is mobile, this configuration will evolve to a point where the base of the craton and the base of the oceanic plate are at nearly the same temperature. As a result, the temperature along the near-vertical craton boundary will be almost uniform. This vertical-wall boundary is an unstable condition and will generate small-scale flow (Figure 2).

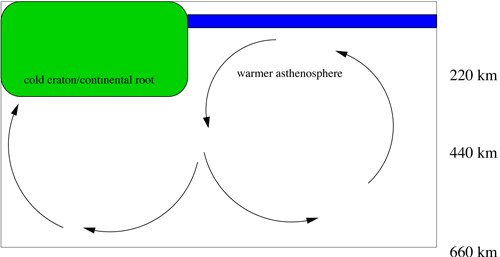
Figure 2: Cartoon illustrating the small-scale convective flow field from the EDC instability along a craton boundary. The EDC instability is driven by the temperature discontinuity at the vertical wall separating the cold, stable craton from the warmer asthenosphere (King & Anderson, 1998).

The arrows in the cartoon illustrate the resulting flow pattern in the absence of other upper-mantle instabilities or large-scale plate flow. This is similar to the flow pattern that forms deep-water masses at the edges of the polar ice shelves. (The deep-water-mass formation problem is more complex because the freezing and melting of seawater affects not only the temperature but also the salinity of the water.) Because this is a short-wavelength flow pattern, the endothermic 660-km phase transformation acts as an efficient barrier to the flow (Tackley, 1996). Given the nature of convective instabilities (Turcotte & Schubert, 1982), the flow would naturally adopt a horizontal wavelength similar to (i.e., 1-1.5 times) the depth (~ 600 km). Therefore it is reasonable to expect that weak upwellings 600-1,000 km from the craton boundary result from EDC.

The EDC calculations illustrated below are computed using a compressible convection formulation for a two-dimensional Cartesian geometry (Figures 3 & 4). These represent our attempt at the most realistic parameters for the upper mantle. The calculations are performed in a 2,890 by 2,890 km domain with 256 bilinear elements in each direction, although only a subregion of the domain is shown. The Rayleigh number used is 2.5 x 10⁷, a reasonable approximation for Earth. The parameters are chosen so that the resulting surface heat flow approximates the mean surface heat flow of Earth. The initial thermal structure of an ocean basin is calculated using the solution for a moving plate, while the thermal structure of the cratonic lithosphere is calculated using the half-space solution and assuming that the craton is uniformly 500 Ma.

No attempt has been made to address the composition of the craton at this point. The cratonic root is assumed to be highly viscous and neutrally buoyant as required for cratonic root stability (e.g., Shapiro et al., 1999a; Lenardic & Moresi, 1999). The calculations also contains solid-solid phase transformations at 410 and 660 km depth, which confine EDC to the upper mantle. The Clapeyron slopes used for these phase changes are 3.5 K/MPa (at 410 km) and -2.8 K/MPa (at 700 km), consistent with the values of the olivine to wadsleyite phase transformation (at about 410 km) and the ringwoodite to perovskite plus magnesiowüstite phase transformation (at about 660 km). There is an additional factor of 30 increase in viscosity at 700 km depth. This viscosity profile is consistent with many geophysical estimates of mantle rheology. The viscosity of the fluid depends on pressure and temperature, but not stress, following the creep properties of olivine.

The location of the craton with respect to the edges of the computational domain is fixed in each calculation. The distance between the edge of the craton and the ocean ridge is varied from 400 to 1,600 km in a series of calculations to study the pattern of the small-scale flow as the width of the ocean basin is increased. When the ocean basin is narrow (Model A, Figure 3 top), an upwelling forms along the edge of the computational domain, which represents the central spreading axis of the ocean basin. A downwelling forms beneath the craton, slightly craton-ward of the craton-ocean margin. As the width of the ocean basin increases with time (Model B, Figure 3 bottom), the upwelling moves off the spreading axis while the downwelling remains fixed with respect to the craton-ocean boundary. The resulting EDC cell is at most 800-1,000 km wide regardless of the location of the craton. EDC reaches a peak velocity of about 30 mm/yr after about 80-100 Myr. After 100 Myr the vigor of the flow slowly decreases (compare Figure 4 top (20 Myr) and bottom (100 Myr)).

When applying the EDC hypothesis to specific cases, it is important to consider that the EDC instability is relatively weak and can be overwhelmed by flow due to other temperature anomalies in the upper mantle, relative motion between the craton and upper mantle, or general plate-scale flow (c.f., King & Anderson, 1998). This might explain why hotspots could be associated with the African cratons via EDC, as suggested by King & Ritsema (2000), while at the same time similar features (hotspots or upper-mantle seismic anomalies) are not observed at most other cratons. The African cratons are ideal for EDC because they are far from subduction zones and other “active” features of mantle flow and may be relatively stationary with respect to the upper mantle.

Effects of continents and cratons that can lead to small-scale convection yet differ from EDC

There have been a number of suggestions that (super)continents may effectively “insulate” the upper mantle, leading to a buildup of heat (Gurnis, 1988; Anderson, 1994; Lowman & Jarvis, 1995; 1996). This lateral variation in temperature between the warm, insulated mantle beneath the (super)continent and “normal” upper mantle can drive an upper-mantle convective flow pattern. This continental insulation flow, is not the same as the EDC flow pattern described above, although it is the primary source of buoyancy driving the convective flow pattern seen in the calculations presented by King & Anderson (1995). With continental-insulation flow, the upper mantle beneath the continental lithosphere is hotter than the upper mantle beneath the oceanic lithosphere.

The pattern of flow resulting from continental insulation is opposite to that of EDC flow (Figure 5). In addition, the wavelength of this flow depends on the wavelength of the upper mantle temperature anomalies. Thus, continental insulation temperature anomalies can be much broader than those associated with EDC but, they not likely to form beneath isolated cratons or even small continents. Anderson (1982, 1998) suggests that continental insulation can increase the upper mantle temperature by as much as 200°C. Based on our simple modeling (King & Anderson, 1995, 1998) a large-scale, 200°C anomaly would drive a major upper mantle convection cell and would most likely wipe out any EDC effects. At the initial stages of rifting of a continent, upwelling should occur as warm mantle from beneath the continent occupies the space created by the spreading continental masses. The active rifting will dominate until the “edges” develop. EDC flow could develop once the continental or cratonic “edge” has migrated some distance from the forming rift.

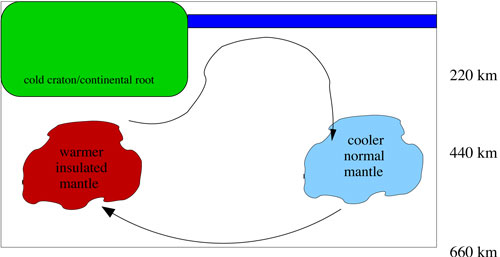
Figure 5: A cartoon illustrating the small-scale convective flow field resulting from lateral temperature anomalies in the upper mantle due to continental insulation (c.f., King & Anderson, 1995).

It is important to point out that continental insulation may be a rather unusual situation, requiring large continental areas (supercontinents) that are stable for a long period of time. Lowman & Jarvis (1996) suggest that rather than thermal insulation, the mechanism for warm upper mantle beneath large supercontinents may be upwelling “return” flow beneath the continent resulting from subduction which often surrounds supercontinents. It is possible that the upper mantle beneath the former Pangea is still warmer than average, with some effect from “insulation” the continent.

Finally, lithospheric delamination could also generate an upper mantle scale flow. It is difficult to maintain a deep continental root in convective models (c.f., Shapiro et al., 1999b) although one can argue that the geophysical evidence suggests their stability is less difficult for the Earth than it is for numerical modelers. Progress is slowly being made (e.g., Shapiro et al., 1999a; Lenardic & Moresi, 1999; Lenardic et al., 2003). The flow generated by lithospheric delamination is illustrated in Figure 7. I include this case primarily to illustrate that EDC and lithospheric delamination are different. (See also Lithospheric Delamination page)

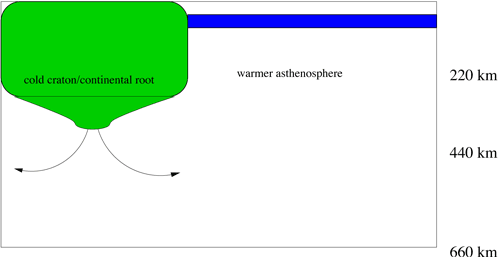
Figure 7: Cartoon illustrating the small-scale convective flow field resulting from the delamination of the sub-cratonic lithosphere root (c.f., Shapiro et al., 1999b).

All of the upper-mantle, “top-down” instabilities described here are illustrated in ideal situations without plate-scale mantle flow or moving plate boundaries. Both of these effects are likely to complicate the resulting upper-mantle flow. Additional factors that could be important include the mechanism that stabilized the continental root or tectosphere (mechanical or buoyant) and the thermal profile of the continental lithosphere and root (e.g., the distribution of heat-producing elements – see also Energetics page). Because this mechanism has only begun to be explored, it is difficult to place limits on which cratonic edge boundaries could generate and EDC flow. In addition, the cartoons shown here illustrate fairly simple, 2D flow geometries. There has been almost no investigation of 3D, top-down flow. However, we can draw on experience with 3D convection to speculate on the important effects.

The direction of the “background” or large-scale mantle flow (or similarly, the differential motion of the continent-craton relative to the upper mantle) can retard or wipe out an EDC instability. King & Anderson (1998, Figure 3) show that large-scale mantle flow that moves from the oceanic plate toward the craton can overwhelm the upwelling “return” part of the EDC cell, effectively wiping out the EDC flow. The EDC upwelling will separate into distinct, 3D quasi-cylindrical upwellings. When aligned with plate motion, as in the case of the Bermuda swell discussed by Vogt (1991), it is possible that the upwelling planform would be more of an elongate upwelling (i.e., sheet) perpendicular to the direction of plate motion. The shape of the observed seismic velocity anomaly beneath Iceland (Foulger et al., 2000, 2001) is consistent with the shape expected from EDC flow generated by the Greenland and/or European craton edges; however, there are no fast seismic velocity anomalies in the upper mantle tomography models of the North Atlantic region below these craton boundaries.

Top-down instabilities will be more prominent if there is a decoupling of the plate-scale flow from the rest of the mantle. A low-viscosity zone beneath the oceanic lithosphere, consistent with a number of mantle viscosity models (c.f. King, 1995) would likely decouple the plate-scale flow from the rest of the mantle (Han & Gurnis, 1999), including top-down instabilities.

It is intriguing that in the North Atlantic, the youngest and narrowest part of the Atlantic basin, hotspots occur on the ridge axis (Iceland and Azores), while in the Central and Southern Atlantic there are a significant number of off-ridge hotspots (Bermuda, Mederia, Canary Islands, Cape Verde, Frenando, Arnold Seamount, Trindade, Mt. Cameroon, Vema). This is also consistent with the predictions of EDC. Applying EDC “theory” to the opening of the North Atlantic, I envision the following series of events. The initial rifting of Pangaea is accompanied by excessive volcanism because of the warmer-than-average mantle beneath the Pangaea supercontinent (continental insulation flow, King & Anderson, 1995). The Tertiary basalt provinces form at this time. As rifting approaches craton boundaries the mantle upwells from deeper (beneath the craton) and the amount of decompression melting increases. In addition, rifting through the craton occurs more slowly. Both effects lead to further increased volcanism and the development of flood basalts (Paraná-Etendeka). As the Atlantic forms and opens, EDC begins along the craton edges (King & Anderson, 1998). When the width of the Atlantic exceeds 2,000 km the EDC flow is no longer captured by the passive ridge flow and the off-axis Atlantic hotspots form (Bermuda, Mederia, Canary Islands, Cape Verde, Frenando, Arnold Seamount, Trindade, Mt. Cameroon, Vema).