Roadmap | The review process | Home
 
Seismic structure of the mantle beneath Hawaii: Discussion

4th December, 2009, Bruce Julian
You can figure out the resolution length for 10-20 s SKS waves on the back of an envelope. It is the diameter of the first Fresnel zone, given by sqrt(Lλ), where L is the ray-path length and λ is the wavelength. L is of the order of the radius of the Earth, and λ is about 100 km (20 s x 5 km/s), so the answer is about 700 km. (Or you could just look at the sizes of the blobs in Figures 7-10 of Julian (2005). These are for 40-s ScS, so they are somewhat larger.) This distance is the size of the zone that a seismic wave "feels". Since SKS seismic rays are approximately vertical, the horizontal resolution in a tomography study might approach this figure, but the vertical resolution will be much worse.

Julian, B. R. (2005), What can seismology say about hot spots?, in Plates, Plumes, and Paradigms, edited by G. R. Foulger, J.H. Natland, D.C. Presnall and D.L. Anderson, pp. 155-170, Geological Society of America.

22nd December, 2009, Andy Moore
I was very intrigued by this paper. You show a figure of a mantle section which included what I presumed is the putative plume, although this was not in the actual paper. If you have a pdf/jpeg copy of this figure at a larger scale, would very much appreciate seeing this. What intrigues me is that the plume just seems to die out at depth, and could not be traced to the core/mantle boundary. Maybe it is getting beyond the limit of seismic detection? But I wonder whether this is in fact what would be expected with the old Turcotte/Oxburgh membrane concept, with stress release melting caused by plate motion occurring at some depth in the mantle. In other words, are we not mixing up an active plumbing system linked to an active volcanic centre with a plume, and claiming that the plumbing system represents the plume? The proverbial chicken and egg in other words?

23rd December, 2009, Don L. Anderson
Andy Moore’s comment gets at several issues involved in the plume debate. First is the scale of normal convection vs. the scale of putative plume convection. “Normal” mantle convection is driven by internal radioactive heating, secular cooling and by heat conducted to the surface through a thermal boundary layer. The scale of this convection is measured in thousands of kilometers and involves temperature anomalies of hundreds of °C. Superposed on this, in the plume hypothesis, is an independent  hypothetical smaller scale (< 200-km) and hotter (> 200°C) form of convection that is driven by core heat. Both forms involve buoyant upwellings, which define plumes in the fluid dynamic literature.

“Mantle plumes”, as defined by Morgan, Campbell, Davies and others differ from normal convection in scale, origin and temperature. For example, dikes, midocean ridges, backarc basins and mantle displaced upwards by sinking slabs or flux-induced melting (also called “plumes” in fluid dynamics) are all upwellings but are parts of plate tectonics and normal convection, rather than being independent of these, as in the mantle plume hypothesis. There is abundant evidence for the normal or plate-scale of convection, including upwellings, but very little evidence for hotter narrower upwellings. Related to this issue is whether all low-seismic-velocity regions in the mantle should be considered hot and buoyant, and referred to as “plumes”.

Second, magmatism requires a source of magma and suitable stress conditions in the overlying plate. If the asthenosphere is above or near the melting point, extension will result in cracks, dikes and magmatism. The membrane hypothesis was one idea about the source of extensional stress but there are others, both global and regional. Global stress maps show that ridges, backarc basins, rifts and "hotspots" all occur in extensional regions, often along pre-existing fractures. Surface-wave data show that the upper 120 km of the plate under Hawaii is normal in all respects and that the asthenosphere, while having low seismic velocities, is less slow than under ridges and backarc basins. A cracked lithosphere satisfies the geophysical data and explains the scale of volcanoes without assuming similar scale thermal anomalies.

Third, there are very few seismic rays that emerge at Hawaii that also sample the deep mantle under Hawaii, and none of these are used in recent seismic studies. Having an array of ocean bottom seismometers around Hawaii does not help. But it is true that when suitable data are available, such as at Yellowstone, Changbai, Iceland and Eifel, the low seismic velocity features do indeed die out at depths ranging from 200 to 650 km. The bottom and depth extent of such features cannot be determined if only steep rays (S, SKS) are used. Geophysical data do not require deep high temperature upwellings under hotspots; shallow fertile regions are indicated.

Global studies show that the central Pacific has lower seismic velocities than average over much of the upper mantle and top of the lower mantle. The scale of the low velocity region is thousands of kilometers and may be part of normall large-scale mantle convection. It does not show up in the geoid or in global maps of mantle density and is therefore not a thermal upwelling, but even if it is, it does not satisfy the Morgan-Campbell constraints of mantle plume upwelling.

Checkerboard tests show that alternating low and high velocity anomalies with depth will be smeared into one continuous LVA when near-vertical rays are used. This critical test is not performed by Wolfe et al. (2009) who use vertical prisms instead, with continuous low-velocity anomalies with depth.

I have prepared a short Powerpoint tutorial that may be of interest.

4th January, 2010, Don L. Anderson
Resolution tests
It is not generally appreciated, apparently, that near-vertical teleseismic waves (S, SKS, P. PKP, ScS, Sdiff) have limited capabilities for determining absolute velocities and depths of anomalies. Those studies that use relative arrival times (e.g., Wolfe et al., 2009) have no constraints whatsoever on whether the underlying mantle is slow or fast.

Simple arithmetic shows that vertical rays traversing a checkerboard test pattern composed of alternating high and low velocity blocks, with equal relative velocity perturbations and zero mean, will end up with a delay, or positive residual. This is because the rays spend more time in the low velocity blocks. This prediction is confirmed by elaborate checkerboard tests of rays emerging at Hawaii (Lei & Zhao, 2005). If the test pattern has equal and opposite temperature perturbations, the predicted slow anomalies are even more effective because of the non-linear effects of temperature on seismic velocity. Velocity lowering is even more extreme if the temperature excursions lead to melting. The net result is that inversion of teleseismic arrivals to Hawaii cannot help but find a low velocity cylinder under Hawaii...even under ideal checkerboard conditions.

The depth extent of the cylinder depends on the corrections for shallow structure, the allowable velocity perturbations, the effects of anisotropy and smoothing. Wolfe et al. (2009) argue that shear velocity perturbations in the shallow mantle cannot exceed 4%, about half what is observed under Yellowstone, the Rio Grande Rift and the Lau Basin, and much less than observed across fault and suture zones, even ancient ones. This assumption dictates the depth extent of their S-wave anomaly. The depth extent of the SKS anomaly is based on a homogeneous lower mantle and an isotopic upper mantle. Even the relative S-wave variations across the Hawaiian array, the only source of data, are no more than across the Canadian Shield.

More generally, in regions of sparse coverage, such as the Pacific, resolution tests find only the low velocity patches and the whole underlying upper and midmantle will appear to be slow (Li et al., 2008). Normal mode, surface wave and surface bounce data are required to actually determine the velocities in the mantle under the Pacific.

Lei & Zhao (2005) present a test model with a uniform pattern of high and low velocity blocks. Near vertical rays (P, PKP, S, SKS) convert this pattern to a vertical slow cylinder (Lei & Zhao, 2006, p. 438-453).

Contrary to implications in recent papers, relative teleseismic delay times cannot determine absolute seismic velocities or temperatures under Hawaii. They cannot even determine relative velocity perturbations or depths. The data cannot show, as claimed, “that the Hawaiian hot spot is the result of an
upwelling high-temperature plume from the lower mantle" (Wolfe et al., 2009, abstract). The apparent plume tilts downward toward the southeast, in conflict with studies by Montelli et al. (2004) (to the W), Lei & Zhao (2005) (to the S) and Wolbern et al. (2006) (to the NE). The neglect of the unique upper mantle anisotropy around Hawaii (Ekstrom & Dziewonski, 1998) creates an additional delay of 0.8 s in SKS, which Wolfe et al. (2009) attribute to the lower mantle portion of their conjectured plume. Lower mantle structures have been observed to give SKS delays of 6 s, even when S is normal. Shear zones extending to 200 km can give delays of 2 s (RISTRA).

Lei & Zhao (2005) argue that the LVA anomaly under Hawaii (2000 km across!) is continuous to the CMB. This is partially because of their color scale and the orientation of their cross section. Other color scales and other cross sections (e.g., Ritsema, 2005) show that the lower mantle features are disconnected from the upper mantle ones. Map views show that the feature changes shape, orientation, intensity, size…with depth…with the largest change occurring at 600 km, as in Wolfe et al. (2009). If it is a continuous feature it widens as it rises into the low viscosity upper mantle and is therefore not a buoyant upwelling, nor need it be rising. This huge feature, if buoyant, should be evident in residual geoid and topography.

The 650 km discontinuity should be elevated substantially in a broad region to the NW of Hawaii but in fact it is no shallower than it is under ridges or the S .Pacific, depending on author, and shear velocities are not particularly low in the transition zone NW of Hawaii. Wolbern et al. (2006) argue for a SW source (and not a SE source) for the Hawaiian plume, based on elevations of the 650 km discontinuity.

There is also the matter that station residuals for P and S waves to Hawaii are not particularly anomalous.

In summary, regardless of what the mantle under Hawaii looks like, if no mistakes are made, teleseismic data will image a deep low- (relative and absolute) velocity cylinder.

5th January, 2010, John R. Evans
Vertical resolution in teleseismic tomography is (almost) all about the interaction of ray crossfire with anomaly shape. This is also true for resolution in general for all forms of tomography, though additional issues like strong nonlinearity crop up when turning points and strongly-coupled parameters are in the model volume).

For issues related to relative times, perhaps you are thinking of the problem with quasi-horizontal features such as a possible magma pooling at Yellowstone, which I think creates a horizontal, mafic lens of very low velocity near or a bit above Moho. Any such feature will resolve pretty well at the edges ("well" in the sense of contrast, not absolute levels or v(x) shape) and very poorly in the center, eviscerating that into a diamond shape that is very weak but thick in the center, about 1.5 times as high as wide in the crust when using P or S. That central part can be effectively invisible in the model.

The problem with SKS and PKP (not S and P to nearly that degree) is that even well into the upper mantle these rays are very close to vertical–a few degrees off at best–so that adequate crossfire is impossible below the depth of good P and S crossfire–the situation at Hawaii (as Wolfe et al. (2009) point out, but then go on to push interpretations beyond the capabilities of the data). For this reason, the 1500-km deep smear of low is quite clearly an artifact derived from shallower, more anomalous structures, or at any rate one cannot demonstrate the contrary, resolution kernels and checkerboards clearly notwithstanding. This is a game of the sum of many small numbers in a noisy, damped system for which numerous approximations and parameterizations have had to be been made. The same holds for the deep NW-dipping anomaly at Yellowstone–pure bunk that no properly experienced tomographer would give a second glance at.

On the issue of diffractions, yes, leading diffractions appear in waveforms recorded "down wind" of a velocity low. But the (visual, correlative, cross checked) methods used by a good tomographer are virtually immune to this problem and readily track the larger direct wave to perhaps 4-5 anomaly-diameters behind the anomaly. I have seen (and ignored) such diffractions in a number of studies.

Unfortunately, most tomographers use the Van Decar & Crosson (1990) wide-window numerical-correlation algorithm to pick and do very little visual cross check and debugging of the new, giant data sets. Unless a method that correlates only the largest early peak or trough is used, this method must subsume significant systematic errors–the very signals used to compute receiver functions as well as diffractions. These systematic errors will map to something in the model and what will be effectively impossible to identify, though probably with a tendency to map toward the top or bottom of the model.

I believe I'm about the 6th person to practice teleseismic tomography on this planet (7th for any form of tomography), and almost certainly am the most experienced of these, with 17 years more or less continuous work, including numerous numerical tests of the method. I fear I have become the dreaded Survey Curmudgeon and am convinced that there still is no-one else out there (except my students!) who fully understand the perils and pitfalls of the technique in its full glory–cf. Evans & Achauer (1993). New techniques (since ACH) have wowed everyone now practicing into a misplaced sense of security in trade for some second-order improvements over ACH (nil improvements over ACH as practiced by Evans & Achauer, 1993).

On how anomalous the upper mantle can get, I'd side with Helmberger for S (perhaps 5% for P) with the addition of suspected lenses like Yellowstone's. At Yellowstone, it is clear that 1 - 1.5 s of the ~2 s intra-caldera P delay is due to the upper crustal anomalies (very strong) and the magma lens (< ~50 km deep) while the upper mantle is consistent with a partial melt +/- melt channels (likely + in Hawaii in the deeper seismic zone).

5th January, 2010, Don L. Anderson
The upper mantle can be as much as 5% slow for P under Hawaii, meaning about 10-15% for S. I think Jimez is about 8% spread over 200 km. Alpine fault is reported to be 35% slow for P (high pore pressure?). Magma/mush can get outrageously slow and, in contrast to dry porosity, this does not get suppressed by pressure. What are the chances that there is a 40 km wide, 200 km deep fissure-mush zone under the Hawaiian volcanic ridge?

If 1 to 1.5 s of delay can be explained by upper crustal anomalies, as at Yellowstone, this would certainly explain the S-delays across Hawaii. 6% anisotropy (Ekstrom & Dziewonski, 1998) can take care of the SKS part.

Incidentally, do we know the absolute travel times to Hawaii? Is S slower than to western North America?

5th January, 2010, John R. Evans
Absolute velocities are utterly invisible with relative residuals. The way that plays out for a thoroughgoing layer of any velocity is that you cannot see it at all. But if one has a discontinuous layer like a lens or the edge of one terrain against another, the contrast can be determined well across the boundary but the shape of the anomaly will be very different. I see no way to get to absolute velocities without lots of turning points and entire raypaths within the modeled volume. This is the case for local-event tomography in which case (x,y,z,t) for events are also in the mix, along with their z-t tradeoffs. All this leads to very badly behaved nonlinearity that has led to numerous garbage results in the literature.

Crossfire and resulting resolution are determined by the ray density and (hopefully minimal) isotropy in the five axes of any ray segment: (x,y,z,a,i). So one wants as many azimuths and incidence angles as possible and as large an array aperture and as dense a station spacing as possible, with smoothness in these things ranging from important to essential. This figure below, from Evans & Achauer (1993), illustrates where one can and cannot expect good resolution.

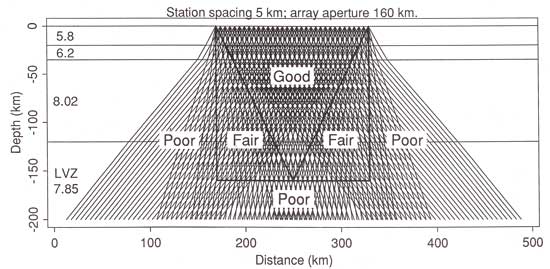
Figure from Evans & Achauer (1993)

Checkerboard tests are not useful, regardless of their popularity.

Core phases do have some nonzero incidence angle. They can help a little, but one must have a well-designed array and a well-chosen set of sources varying broadly in azimuth to recover anything. The primary efficacy of core phases is to add another incidence angle in the region with good mantle-phase crossfire. After that, all one can hope to say (with limited confidence) is that there is something additional out along such-and-such a ray bundle, P(a), S(a), PKP, and SKS. You can have virtually no idea where along that ray bundle it lies, and smearing of shallow features makes even this much dicey.

Anisotropy definitely can have such effects and these would model pretty easily into a vertical smear below the region of good crossfire. It is a poorly explored issue.

A 40 km wide, 200 km deep fissure-mush zone under the volcanic ridge is perfectly plausible but I'd place my bet on artifact for the deep anomaly.

7th January, 2010, John R. Evans
The results are very interesting in the upper 500 km and the array is well enough designed to support that pretty well. However, anything deeper is completely unsupported by the data and the method. Unfortunately, all that shallow interesting and probably OK part is color-saturated in the Science paper and thus not available for interpretation.

It seems the Van Decar & Crosson (1990) picking method was used and it is not clear if the result was human-checked. There may well be additional artifacts from using this picking method incorrectly.

I may have been the first to try stripping off the signal of shallow structure or otherwise forcing modeling within a limited depth range (in order to "see through" strong, shallow anomalies), but I'm not sure exactly what was done here. I am sure such stripping in no way informs whether the artifacts are artifacts, though it might reduce their magnitude. In any case, the initial model space should not extend much below 500 km since nothing isresolved below this depth in any meaningful way (one ignores the bottom layer since that soaks up a lot of the leftover signals that one cannot model properly).

The array is well-designed to support tomography in the upper 500 km, as mentioned above, and a good result can be had from the data. The data set very likely would also work well to reveal any CMB-plume guided phases (think optical fiber: Julian & Evans, in press). Finding such phases would be strong evidence for a CMB plume while not finding them in a data set good enough to see them would be pretty good evidence for the absence of such structure (but not the slam-dunk of finding them). It's the only seismic method I know of that has meaningful potential for finding a weak, long, skinny, deep anomaly.

7th January, 2010, Don Anderson
The total relative S delays in the Hawaii experiment are ~2-3 seconds. It is hard to convert these to absolute delays but absolute P delays to Hawaii order 1 s are not extreme by global standards.

However, the paper of Wolbern et al. (2006), contrived as it is, does show that S wave delays above 410 and between 410 and 650 range up to 3 s, with no lower mantle involved. These of course depend on both velocity and discontinuity depths but they show that maybe there is plenty of variation above 650 or even 400 to explain it all.

7th January, 2010, John R. Evans
Those numbers (P & S) fit reasonably well for shallow partial melts and melt-filled fractures, but I must admit to being a little out of date on the theoretical and lab work on partial melts etc.

9th January, 2010, Alexei Ivanov
Is any chance of getting the essence of these comments published in the white literature?

9th January, 2010, Gillian R. Foulger
I would think that a re-processing of the data would be expected, demonstrating that the claims of poor resolution are true.

11th January, 2010, John R. Evans
The usefully resolved depth of any teleseismic tomography study is approximately equal to the array aperture. The array in question is reasonably well designed for a study reaching ~500 km beneath the big island but not deeper – the data cannot return interpretable results below this depth in the presence of shallow, strong anomalies, notwithstanding efforts to "strip" shallow structure, to remove whatever signal can be attributed to the surface. Stripping can help some, but because the inversion is damped, some of the shallow signal will remain in the observations and will be subject to smearing.

The best-resolved volume in any ("restricted array", i.e., regional) teleseismic tomography is an inverted cone with its "base" at the array at the surface and its vertex beneath the center of the array at a depth about equal to the array aperture. This is the volume in which one can obtain mantle phases from numerous azimuths and moderate incidence angles +/- core phases at near vertical. Even here, the ratio of vertical to horizontal resolution is roughly 0.5 and inhomogeneity in the ray distribution in 4D can cause more than the usual artifacts.

In the remainder of a cylinder beneath the array and of diameter and depth range equal to the array aperture one has mantle phases from a narrow range of azimuths plus a core phase so the resolution is fairly good but with more radial (here, depth) smearing than within the cone. At flatter angles outside this cylinder (larger incidence angles) and below the resolvable depth, the bottom of the cylinder (~500 km here) where there are only separated bundles of rays of nearly the same orientation and there is very little resolution and terrible smearing – this separation is well illustrated by some of the supplementary information provided by Wolfe et al. (2009). At best one can suggest that there is some remaining traveltime anomaly somewhere off in those general directions with no idea where along those separated ray bundles the anomalies lie (yes, including all the way back to the surface at the array). Worse, when the features out there are significantly weaker than the shallow anomalies (cf. recent Yellowstone and Hawaii work) one can have absolutely no confidence in those nil-resolved regions and the presumption must be that those streaks are entirely artifacts of shallower (including upper crustal) anomalies of greater strength coupled with the damping effects of the inversion process (damping will always push the minimum of the model toward more but fainter smearing – "shorter" models – at the expense of a poorer fit to the data). That is, radial artifacts are a necessary result of shallower anomalies resolved by any (effectively-)damped inversion and are taken seriously by no-one well experienced in the method. Ample evidence of such effects are given in numerous figures in Evans & Achauer (1993).

To these problems add the systematic picking errors returned by the method of Van Decar & Crosson (1990) when used with a correlation window wider than about two seconds beginning at or near the first arrival. In the presence of such systematic picking errors, the smearing will tend to worsen; those errors must find a home in the model – be converted into spurious "anomalies" – and the easiest (least otherwise constrained) regions into which to add such spurious signals is in the otherwise nil-resolved region below and beside the stubby cylinder described above and shown in the figure.

The issue of whether smearing can happen with such a data set is already fully answered: smearing always will be present in this class of methods and anomalies; the phenomenon requires no additional demonstration in particulars because it is a well known, well understood effect. Indeed, Evans & Achauer (1993) show a whole series of tests showing the "I on X" smearing patterns to be expected as the norm and the vertical elongation of equant anomalies into roughly 2x1 upright model features.

As we've discussed, these issues do not preclude the possibility of a weak, deeper feature – such features are simply un-demonstrated by the present data and, indeed, cannot be demonstrated with any confidence at all by that data set. It is a potentially great data set for looking at the upper 500 km but useless below that and there should be no other expectation from such studies.

Finally, checkerboard tests of damped inversion schema prove only that it's a damped inversion method – they are useless as tests of resolution, indeed worse than useless because they badly overstate whatever resolving power the data have. This is so because all damped inversion methods prefer to resolve oscillatory structures, even to the extent that if given an ill-constrained starting model/data combination the inversion inevitably will return blocky results, even in the case of pure noise input to the model. (Such blockiness is useful as a symptom of the underdamping of a noisy data set and/or the use of blocks that are too small – that is, of asking too much of the data.) The only meaningful resolution tests I know of are to look at individual resolution kernels (columns of R or the crudely equivalent one-block or -node synthetic models using an identical ray set); several one-block examples should be provided for each of the various regions outlined in the ray figure from Evans & Achauer (1993), reproduced above. Even this exercise is of finite efficacy because of the issues of parameterization, linearization, and long sums of tiny numbers, which can have non-obvious results (which must be assumed present unless otherwise demonstrated ... how is unclear). Call these one-block models or kernels the local "impulse response" of the data set and inversion method but remember the long string of simplifying assumptions built into even these.

29th June, 2010, Don L. Anderson
I have been waiting for someone better qualified than myself to comment in Science or Nature on the Wolfe et al. (2009) Hawaii paper, and and others that basically use a vertical tomographic (ACH) approach to mantle structure. The claims in these papers are compelling to non-seismologists (including journal editors). Most seismologists have gone beyond this type of study but they are still widely quoted, by non-seismologists, and even referred to as "the highest resolution studies out there...". I am working on an Appendix to a current paper and I would appreciate the thoughts of others.

30th June, 2010, Adam M. Dziewonski
Don: It has been known for over 100 years (Herglotz-Wiechert) that you cannot uniquely determine a velocity profile if you do not have data for rays that bottom in a certain range of depths (low velocity zone). What you call "vertical tomography" is an attempt to circumvent this law. This is achieved by assuming a starting model and seeking perturbations to it by imposing additional conditions of minimum norm or minimum roughness.

The problem with studies such as that of Wolfe et al. (2009) is that they infer a structure for which they have only data with a very limited range of incidence angles at lower (and upper mantle depths).

This misconception has been propagated for over 30 years beginning with the 1977 paper by Aki and others. Using teleseismic travel times observed at NORSAR they inferred 3-D structure using rays with a very limited range of incidence angles. In contrast, Dziewonski et al. (1977) also used teleseismic travel times but limited their inversion to the lower mantle, in which it is possible to have all incidence angles from vertical to horizontal.

Structures obtained through inversion of data with a limited range of angles of incidence are highly nonunique, yet the tradition of such inversions continues with dozens of PASSCAL-type experiments. An example is the Yellowstone hotspot, where a slow structure had been claimed at depths exceeding the aperture of the array.

30th June, 2010, John R. Evans
Adam: I think you too overstate the issue but arrive at the correct bottom line (with minor exceptions).

The problem here is not ACH tomography and its numerous (almost exactly equivalent) offspring. The problem is the newbees to tomography (and folks outside that specialty), who do not understand the art and limitations of (restricted array) TT.

It has been known and widely stated from the very beginning that absolute velocities are utterly unknown in TT (and by corollaries that Ellsworth, I, and Uli Achauer established long ago that there are other structures that can effectively disappear or be misunderstood more easily than properly understood (I still think there is a lenticular mafic-silicic "heat exchanger" near Moho at Yellowstone, for example). The tradeoff in full-ray tomography at any scale from exploration to local to global is that the inverse problem becomes highly nonlinear and very sensitive to starting models and how cautious the driver is on that jeep track.

So please don't go throwing out baby with bathwater. TT is a powerful and highly linear, robust (in practice, if in not theory) method with a great deal to offer and has made major contributions where no other method yet dares to go. (Yeah, we'd all love to see full waveform tomography with all sources and constraints from other methods, but it ain't here yet. Even then, I guarantee that it will take 20 years of some curmudgeon like me hacking away to really understand the beast -- there is always more than meets the math.)

The problem is not the method but that newbees forget the art and the geology that are so essential to getting it right and simply go tunnel visioned on the maths, checkerboards, and pretty pictures (scaled for convenience and bias).

Every geophysical method has limitations, which must be well understood or it is useful in, garbage out. The Evans & Achauer (1993) chapter 13 in Iyer's great, pragmatic book on the art of tomography was an attempt to established a Perils and Pitfalls for TT, as was done famously and long ago for reflection seismology (e.g., no, the Earth actually is not composed largely of hyperbole ... only some papers!).

This subject really is worthy of a new paper of its own in a lead journal, a paper redolent in crisp, definitive statements to clarify some things that seem to have been forgotten in recent years.

2nd July, 2010, Jeannot Trampert
Don: I am not sure mere comments are going to change the perception of the subject. There seem to be two camps, the people who understand the limits of the techniques and those who project wishful thinking into the results obtained by the same techniques. There have been many comments and replies in the published literature but the debate has remained polarized.

The problem is of course that we do (could) not estimate uncertainties related to tomographic results. If people knew that anomalies carry uncertainties of the order of 1% (for example), they would refrain from interpreting anomalies of 0.5%. Very often resolution and uncertainty are confused. While there is a relation, they are not the same. You can infer a broad average very accurately, while a local property often carries a large uncertainty.

Checkerboard tests are very dangerous, because they are used to convince people that there is resolution while the mathematics tell you the opposite.

Rather than another comment, I think a tomographic study is needed with a complete uncertainty analysis. We are working on this here in Utrecht, but the calculations are long.

2nd July, 2010, John R. Evans
I agree with Jeannot. R is not C and both subsume a lot of physics and maths assumptions. I hope Jeannot and his colleagues have good success in a better evaluation.

See Can tomography detect plumes? for continuation of this discussion.

References

last updated 2nd July, 2010
© MantlePlumes.org