 |
Effects of lithospheric yield stresses and mantle-heating modes on Pangea breakup |
Masaki Yoshida
Department of Deep Earth Structure and Dynamics Research, Japan Agency for Marine–Earth Science and Technology (JAMSTEC), Japan, myoshida@jamstec.go.jp
This webpage is a summary of: Yoshida, M., Effects of various lithospheric yield stresses and different mantle heating modes on the breakup of the Pangea supercontinent, Geophysical Research Letters, accepted manuscript online: 23 APR 2014 10:36AM EST | DOI: 10.1002/2014GL060023
Geophysical data derived mainly from seismological observations provide details of the structure of the present-day interior of Earth. Geological data obtained mainly from geochemical and paleomagnetic analyses provide information about the history of Earth’s surface. However, such observations and analyses do not embrace the complete depth range from 0 to 6371 km, nor time, which ranges from 0 to 4.6 Ga. Thus, data about Earth’s deep interior in the past, which are crucial to determining Earth’s evolution, are not available [Gerya, 2014], and the geodynamics of the past deep interior remains controversial. Numerical simulation of mantle convection is a possible approach to reconstructing the past Earth’s mantle.
In recent years, plate reconstruction models based on data from geology and geomagnetism, have illustrated the breakup of Pangea and subsequent continental drift [Seton et al., 2012]. In the present study, numerical simulations of three-dimensional (3D) mantle convection was done using the geometry of Pangea at 200 Ma taken from Seton et al. [2012]. The effects of various lithospheric yield stresses and different mantle heating modes, the main parameters controlling mantle dynamics, are investigated in relation to both the breakup of Pangea and subsequent continental drift for the past 200 Myr.
Mantle convection and continental drift are computed numerically using the staggered grid-based, particle-in-cell, finite-volume code ConvGS [e.g., Yoshida, 2013]. The mantle is modeled as a Boussinesq fluid with an infinite Prandtl number confined in a 3D spherical shell geometry with a thickness of 2867 km. Impermeable, shear-stress-free conditions are imposed on both the top and bottom surface boundaries of the shell. Two different modes of mantle heating are considered:
- Case Q1: The mantle is heated both from the bottom and from within by the decay of radioactive elements, and
- Case Q2: The mantle is heated purely from within (i.e., no heat escapes from the core).
Following previous work [Yoshida, 2013], conservation equations for mass, momentum, and energy, which govern mantle convection under the Boussinesq approximation, and the advection equation for the composition, are solved.
In the present model, the geometry of Pangea is imposed. The digital data of the coastline of Pangea at 200 Ma are taken from the work of Seton et al. [2012] and the GPlates 1.3 software (http://www.gplates.org/). The modeled Pangea is initially broken up into seven major continental blocks (Eurasia, Africa, North America, South America, Antarctica, Australia, and India) and the continental boundaries are treated as narrow oceanic domains. The thickness of the modeled Pangea is initially set to 202 km.
First, the supercontinent is fixed spatially until mantle convection reaches a statistically steady state (e.g., until the average temperature and root mean square velocity of the entire mantle saturate) and the distributions of oceanic plate boundaries reach a nearly stable pattern. Then, simulations of continental drift are performed from 200 Ma to the present.
Figure 1 shows the patterns of continental drift in the mantle convection models with mixed heating mode (Case Q1) and with the yield stress of the oceanic lithosphere varying from 80 to 140 MPa. The white contour line shows the temperature anomaly (the deviation from the horizontally averaged temperature) of the upper mantle at a depth of 493 km. The results reveal that the pattern of continental drift to be quite sensitive to the magnitude of yield stress. The different patterns of plate boundaries at 200 Ma (second row showing the viscosity distributions for each model) leads to variety in the final distribution of the continents at 0 Ma.
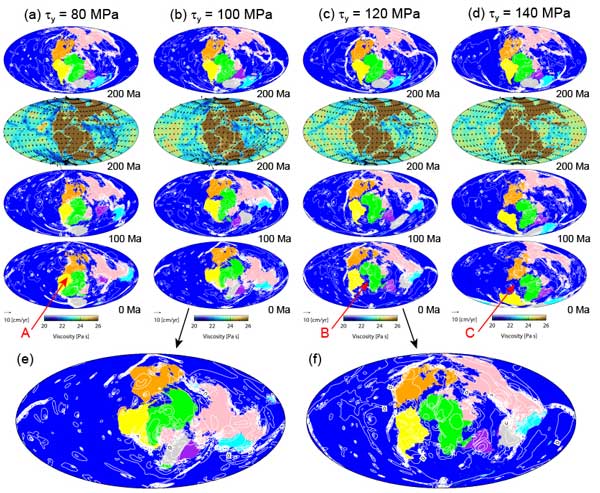
Figure 1: Time sequence of drifting continents for models with mixed mantle heating mode (Case Q1). The lithospheric yield stresss are: (a) 80 MPa, (b) 100 MPa, (c) 120 MPa, and (d) 140 MPa. The first, third, and fourth panels of each figure show the configuration of drifting continents at 200, 100, and 0 Ma. The blue region indicates oceanic lithosphere, and the color-coded region indicates the continents. The white contour line shows the temperature anomaly (i.e. the deviation from the horizontally averaged temperature) of the upper mantle at a depth of 493 km. The contour intervals are 50°C. The solid and dashed lines represent positive and negative temperature anomalies, respectively. The second panel of each sequence shows the distribution of viscosity (color bars at the bottom of each figure) and velocity at 200 Ma. (e and f) close-up views of the fourth panels of (b) and (c), respectively.
When the yield stress is low (80 MPa) and the oceanic lithosphere is greatly damaged, breakup of South America, Africa, and North America does not occur (arrow A in Figure 1a). This is because weak plate boundaries tend to develop broadly along the Pangea margin, and these boundaries absorb the tensional force causing Pangea breakup. On the other hand, the moderate breakup of South America, Africa, and North America occurs in the model when an intermediate yield stress is applied (120 MPa – arrow B, Figure 1c).
When the yield stress is large (140 MPa) and the oceanic lithosphere is less damaged, breakup of South America, Africa, and North America is enhanced (arrow C, Figure 1d). This is because weak plate boundaries are less developed in the oceanic lithosphere at 200 Ma and thus each continental block moves relatively easily for 200 Myr under the action of horizontal motion of mantle convection under Pangea.
Figure 2 shows continental drift on mantle convection with purely internal heating and an adiabatic bottom boundary (Case Q2). The results reveal that the continental blocks of Pangea break up and drift even when active mantle upwelling does not originate at the core-mantle boundary, and when the oceanic lithosphere for each yield stress is less damaged than for Case Q1.
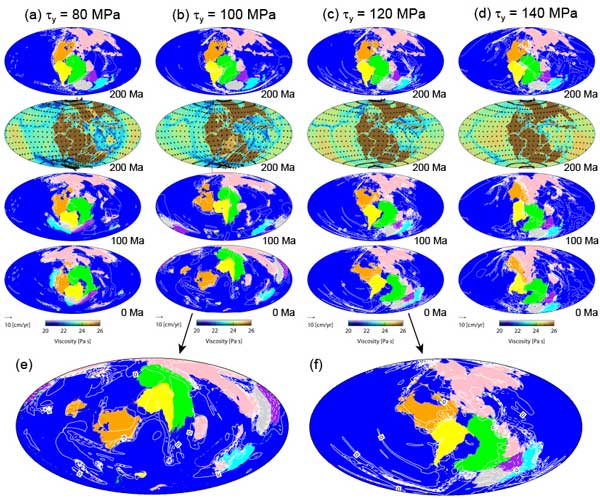
Figure 2: Same as Figure 1 but for models with purely basal heating mode of the mantle (Case Q2).
As illustrated by the model with two different mantle heating modes (Case Q1), it appears that the breakup of Pangea is accomplished with small yield stress, and the preferred yield stress of the oceanic lithosphere is ~120 MPa. Indeed, when the yield stress is larger than 140 MPa (e.g., 200 MPa), continental breakup does not occur for models with two different mantle heating modes because the oceanic lithosphere is even less damaged.
The present study reveals that continental drift following Pangea breakup is very sensitive to the magnitude of yield stress and the mode of mantle heating. This implies that continental drift occurs under limited geophysical conditions. In previous numerical studies [e.g., van Heck & Tackley, 2008; Foley & Becker, 2009], the yield stress has been chosen on an ad hoc basis to obtain the preferred plate-like behavior on mantle convection without continents. The present study suggests that the yield stress of the oceanic lithosphere should be chosen carefully to obtain realistic continental drift.
To reconstruct the present-day distribution of the six continents in numerically simulated mantle convection, it may be necessary to impose artificially the positions of both the subduction zones around Pangea and upwelling regions in the initial state of the simulation by trial-and-error. This was performed by Baumgardner [1993] using a 3D mantle convection model with rigid (non-deformable) blocks representing Pangea. He imposed several upwellings under the present-day Indian and Atlantic oceans to cause the efficient break up of Pangea [Baumgardner, 1993, Figure 5].
Global numerical models of mantle convection provide a unique approach for investigating the behavior of Earth's mantle in the past. The bound on the yield stress derived in the present study will potentially enable the self-consistent reconstruction of continental breakup and drift as well as the accompanying pattern of mantle convection for the past 200 Myr. This may help to answer questions such as the dynamic role of continental drift since 200 Ma on the generation of degree-two thermal heterogeneity in the present Earth’s mantle.
References
-
Baumgardner, J. R. (1993), 3-D numerical investigation of the mantle dynamics associated with the breakup of Pangea, in Flow and Creep in the Solar System: Observations, Modeling, and Theory (NATO Science Series C), edited by D. B. Stone and S. K. Runcorn, pp. 207-224 , Kluwer Academic Publishers, Netherlands.
-
Gerya, T. (2014), Precambrian geodynamics: Concepts and models, Gondwana Res., 25, 442-463, doi:10.1016/j.gr.2012.11.008
-
Foley, B. J., and T. W. Becker (2009), Generation of plate-like behavior and mantle heterogeneity from a spherical, viscoplastic convection model, Geochem. Geophys. Geosyst., 10, Q08001, doi:10.1029/2009GC002378.
-
Seton, M., et al. (2012), Global continental and ocean basin reconstructions since 200 Ma, Earth-Science Rev., 113, 212-270, doi:10.1016/j.earscirev.2012.03.002.
-
van Heck, H. J., and P. J. Tackley (2008), Planforms of self-consistently generated plates in 3D spherical geometry, Geophys. Res. Lett., 35, L19312, doi:10.1029/2008GL035190.
-
Yoshida, M. (2013), Mantle temperature under drifting continents during the supercontinent cycle, Geophys. Res. Lett., 40, 681-686, doi:10.1002/grl.50151.
last updated 23rd May, 2014 |
