 |
Wave-front healing and imaging mantle plumes |
Jeroen Ritsema
Department of Earth and Environmental Sciences, University of Michigan, Ann Arbor, MI 48109, USA, jritsema@umich.edu
This webpage is a summary of: Hwang YK, Ritsema J, van Keken PE, Goes, S, & Styles E (2011). Wavefront healing renders deep plumes seismically invisible. Geophys. J. Int. 187 273–277.
Joint geodynamic-seismic modelling indicates that shear waves propagating through a lower-mantle plume stem are delayed by 0.1−0.2 s at most. This is much less than typical measurement errors and the uncertain contributions to delay times from earthquake mislocations and anisotropy and velocity heterogeneity in the lithosphere. Plume tails in the lower mantle thus cannot be imaged using earthquake arrival-time delays.
Since W.J. Morgan [1971] proposed that intra-plate volcanism can be explained by plumes rising from the lower mantle, seismologists have actively sought physical evidence for them. Although many seismic images have been obtained that show low-velocity anomalies beneath hotspots extending deep into the mantle [e.g., Ritsema & Allen, 2003; Montelli et al., 2004; Wolfe et al., 2009], it remains questionable whether these observations can be uniquely linked to plumes. Simulations [e.g., Ito & van Keken, 2007; Ribe et al., 2007] predict that plume tails are narrower than 100–200 km in the upper mantle. Plumes may be wider than 1000 km in the lower mantle, but their wave-speed reductions are less than one percent. Hwang et al. [2011] demonstrate that the recorded delays of seismic waves traversing such plume tails in the lower mantle are immeasurably small. This webpage summarizes the main points of this study.
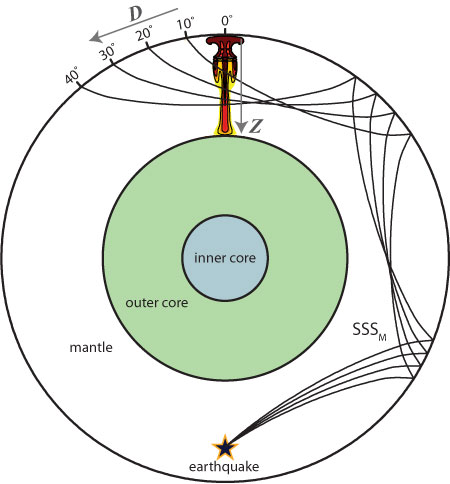
Figure 1: The 3D numerical grid of shear-velocity variation, which has rotational symmetry about the radial axis passing through the plume axis and the earthquake (star) at the antipode. Earth’s layered velocity structure is taken from the PREM model. The plume P0h is shown as shear-velocity perturbations (i.e. low-velocity anomalies) with respect to PREM. The black lines are four geometric ray paths of the major-arc SSS phase (SSS) for epicentral distances of 190°, 200°, 210°, and 220°, which correspond to angular distances D from the plume axis of 10°, 20°, 30°, and 40°, respectively. The ray-geometric crossing depths Z at the plume axis for these distances are 1077 km, 1563 km, 1857 km, and 1989 km, respectively.
Hwang et al. [2011] consider six plumes with different morphologies. These plume models are generated by solving the coupled Stokes and energy equations for thermally-driven convection in a high-resolution axisymmetric spherical shell with modifications for the effects of compressibility and phase changes [Styles et al., 2011]. Phase equilibria, density, and elastic parameters are calculated as a function of temperature, pressure, and composition [Connolly, 2005] and 3D shear-wave (SH) propagation is simulated through the seismic structure of the plumes using the SHaxi method [Jahnke, et al. 2008] (Figure 1).
Figure 2 compares SHaxi seismograms for angular distances D between 1.5° and 9.5° computed for PREM and a model that includes the shear-velocity perturbations of the plume P0h. As expected, the SSS wave is delayed with respect to PREM if it propagates through the plume. When D < 2.5° and SSS traverses the plume head, delay times are larger than 5 s. The delay times diminish rapidly to less than 0.2 s at D = 9° when SSS traverses the plume tail at a depth larger than about 1000 km. The travel-time delay and the form of its decay depend on the morphology and shear-velocity structure of the plume. However, for all plume morphologies investigated, the delay time diminishes with increasing D.
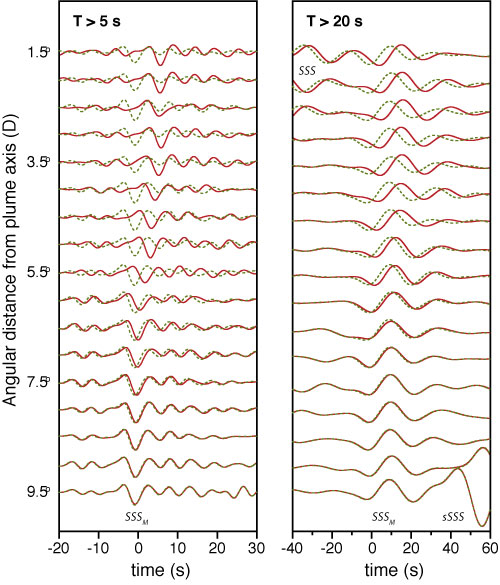
Figure 2: Waveforms (left) for periods longer than 5 s and (right) for periods longer than 20 s of SSS (aligned at time 0) between distances D = 1.5° and 9.5° for models PREM (dashed line) and plume P0h (solid line). The labels SSS and sSSS indicate the signals of the minor-arc SSS and its surface reflection sSSS within the time window around SSS.
The decay of the delay time with increasing D is well understood theoretically by an effect known as "wavefront healing" [e.g., Wielandt, 1987; Nolet & Dahlen, 2000]. After the deceleration of the wave front during its propagation through the plume, the indentation of the wave front gradually disappears as a result of diffraction, and the wave travel-time delay decreases exponentially. Just after traversing the plume, SSS may be delayed by several seconds but this delay has diminished to zero by the time the SSS phase has reached the seismic station on the surface.
Typical measurement uncertainties exceed 0.5 s. These are due to noise, waveform variability, uncertainties in earthquake location and origin time, and the poorly constrained effects of anisotropy and the heterogeneous crust on waveforms. Therefore, maximum delay times of 0.2 s caused by plume tails in the lower mantle cannot be detected. Whilst bodies such as the large, low-shear-velocity provinces [Garnero & McNamara, 2008] in the lowermost mantle are robustly detected, lower mantle, Morgan-type plumes cannot be resolved with seismic data.
References
-
Connolly JAD (2005). Computation of phase equilibria by linear programming; a tool for geodynamic modelling and its application to subduction zone decarbonation. Earth Planet. Sci. Lett. 236 524–541.
-
Garnero EJ & McNamara AK (2008). Structure and Dynamics of Earth's Lower Mantle. Science 320 626–628.
-
-
Ito G & van Keken PE (2007). Hotspots and melting anomalies, in Treatise on Geophysics, (ed. Bercovici D, 7 371–436 Elsevier, Amsterdam.
-
Jahnke G, Thorne MS, Cochard A & Igel H (2008). Global SH-wave propagation using a parallel axisymmetric spherical finite-difference scheme: application to whole mantle scattering. Geophys. J. Int. 173 815–826.
-
-
Nolet G & Dahen FA (2000). Wave front healing and the evolution of seismic delay times. J. Geophys. Res. 105 19043–19054.
-
Ribe N, Davaille A & Christensen UR (2007). Fluid dynamics of mantle plumes in Mantle plumes (ed. Ritter, J. & Christensen, U. R.) 1–48, Springer, Berlin.
-
-
-
Wielandt E (1987). On the validity of the ray approximation for interpreting delay times, in Seismic Tomography, ed. Nolet G., Reidel, Dordrecht.
-
last updated 3rd September, 2012 |
