 |
Why the Rayleigh Number is inapplicable to Earth’s Mantle |
Anne M. Hofmeister1, Everett M. Criss2†
1Dept. Earth & Planetary Sciences, Washington Univ., St. Louis, MO 63130, USA; hofmeist@wustl.edu
2Panasonic Avionics Corporation, Lake Forest, CA 92630, USA; ecriss@eng.ucse.edu
†
This webpage highlights the study of: Hofmeister, A.M. and Everett M. Criss. How properties that distinguish solids from fluids and constraints of spherical geometry suppress lower mantle convection. Journal of Earth Science 29, 1-20.
Models are used to understand observations. Applying a physical theory to a phenomenon requires that the theory’s assumptions are compatible with the situation being modeled. A theory may be valid, but not germane. For example, quantum mechanics or relativistic mechanics do not govern the trajectory of a rocket traveling from the Earth to the Moon, but Newtonian mechanics does. Some choices of the model are less obvious. Our paper explores whether the formulation of Rayleigh (1916) for convective instability is appropriate to the Earth’s mantle. Through considering the underlying assumptions, our paper shows that the Rayleigh criterion is insufficient to predict the existence of convective motion of solid material. Our mathematical analysis provides a new criterion for solids in addition to a minimum size of the Rayleigh number (Ra), and shows how Ra needs to be modified to address the spherical nature of the Earth and how solids behave differently from liquids and gases. Our published mathematical analysis is based on the principles of physics and our findings are verified through comparison with laboratory data.
Our results do not contradict observed plate tectonics, because plate tectonics only requires fluidity and motion close to the Earth’s surface. Plate tectonics does not require whole mantle convection. Furthermore, the whole mantle convection model is not sufficiently supported by observable data. Evidence of the motions of plates down to 660 km is the occurrence of earthquakes there, but this is not the case for the deeper, lower mantle. Another important discrepancy between the whole mantle convection model and our observations is the lack of evidence for thin plumes, such as the one proposed to underlie Hawaii. This is of great concern to whole mantle convection proponents (e.g., Bercovici et al., 2015) because some type of plume accompanies many convective systems. These first-order problems exist even after ~40 years of modelling efforts. Importantly, a mechanism for plate tectonics is not described, and no heat source sufficient to drive mantle convection has been proven. These, other first-order problems described by Bercovici (2015), and the issues set forth on www.mantleplumes.org point to the need to reconsider the basic physics involved in such models. Our paper provides a new, pertinent, mathematical derivation of the Rayleigh number and a discussion of materials science literature. This webpage explains elementary, fundamental concepts.
The whole mantle convection hypothesis rests on the large estimated size of Ra (~108) for Earth’s whole mantle (the 2890 km distance between the surface and the core). Ra for the continental crust computed using properties typical of this layer gives a value of Ra of ~50,000, which is far above the minimum value of ~1700 for convection. And yet the continental crust does not convect. Thus the Ra number of the lower mantle being large may not be sufficient evidence to demonstrate convection.
What did Rayleigh assume? The original derivation of Rayleigh (1916) was an attempt to characterize liquid behavior. This is hardly surprising as ships dominated transport at that time. Liquids behave differently from solids, as is taught very early in scientific education. One key difference is that solids melt when their internal temperature exceeds their melting point. After this phase transition occurs, motions, including convective circulation, are easily stimulated.
Rayleigh assumed that the motions of the medium were brought about by thermal buoyancy only. In contrast to liquids, solids must be significantly stressed to flow. Liquids like water flow downhill with even the slightest tilt. The requirement of force to move solids is evident in the home during use of a garbage compactor. Volume reduction is not the only change in a garbage compactor: the solids can also change shape, because the applied force is not uniform in all directions. Also, tough solids like a bone will not change shape, but softer things, e.g., a piece of cheese, will warp (deform) around the stronger solids. Non-uniform force in scientific terms is called stress. How much stress is needed for deformation depends on the material. For example, munster cheese, a soft cheese, will deform at far lower stress than does a block of hard cheddar. Importantly, deformation implies non-elastic behavior, where the solid does not return to its original shape after the stress is removed. More succinctly, above a certain stress the solid yields, but below a certain stress a solid responds elastically and reversibly. The mechanical behavior of cheese is discussed in terms of an activation energy by Kim et al. (2015) and in terms of a yield stress by Luyten (1998).
Regarding convection of a solid, the material must be able to deformation and flow. Due to the great hardness and strength of rocks, the yield stress is necessary to describe their behavior. Furthermore, it is not volume reduction under hydrostatic conditions that is important, but the difference between the applied, directional forces and hydrostatic compression, i.e., the deviatoric stress. On this basis, our paper proposed that:
Deviatoric stress must exceed the yield stress of material for a solid to convect — (1)
Our contention is supported by data and theory in materials science, such as the concept of an ideal Bingham plastic, and the large effect that grain-size has on deformation of solids (e.g., Meyers & Chawla, 2009). Grain-size is irrelevant to liquids and to the Ra number. Hence, a high value of Ra is no guarantee of convective instability of a solid system.
Deformation studies of rocks and mineral composites provide confirmation. These are conducted at differential stresses of ~100 MPa. Such conditions are outside the elastic regime (see Figure 8 in our paper). In contrast, the lower mantle and much of the upper mantle experience hydrostatic conditions, or nearly so, and thus the Earth’s mantle appears to be inside the elastic regime. This conclusion is supported by seismic measurements, which provide data on the interior of the Earth from compression and shear waves induced by earthquakes, and by comparing the results to laboratory measurements of elastic properties (e.g., Anderson, 2007).
Once stress is sufficiently high, a solid will move in a similar manner to a fluid. Under high stress conditions, rocks do deform. Actually, the rocks creep. However, the results of such experiments are cast in terms of the material property of viscosity, which represents resistance to flow, and is part of the Ra number (discussed further below). As discussed in our paper, considering solid creep to be analogous to liquid flow is an underlying mistake in current models. Solids may creep, but they eventually harden or fail, while liquids flow indefinitely. This difference exists because the mechanisms behind solid deformation and liquid flow are different.
Another crucial difference between Rayleigh’s analysis of instability and planetary conditions is geometry, because this affects conservation of mass. For the Cartesian system (a box) considered by Rayleigh, equal thickness layers with the same density have the same mass. However, this is not true in cylindrical coordinates since area is proportional to radius (Figure 1). For a sphere, area is proportional to radius squared. Thus, Ra for a sphere must include two length scales—it is not only the layer thickness which is relevant—the radius of the object is equally important. Conservation of mass inhibits convection in a sphere, because a volume of rock must thin as it rises. In convection models, non-dimensionalizing the equations of motion and with the Cartesian definition for Ra, which only includes a single length scale and not the body radius, violates mass conservation. Energy conservation is similarly affected, as discussed in our paper.
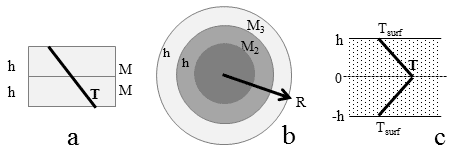
Figure 1: Schematics in two dimensions, showing that geometry is important to mass conservation and instability. (a) Temperature profile inside a box heated at the bottom, which also shows that layers of equal thickness have equal mass. (b) Cross section of a cylinder, showing that equal-thickness layers have more mass when the layer is towards the outside. (c) A box with internal heating, showing that the bottom half of the box is stable against convection (hot liquid over cold), whereas the top half is unstable (cold liquid over hot), as occurs in the bottom heated configuration shown in (a).
A different type of geometric error has been introduced in mantle convection formulations with internal heating. The original Ra number depends on the temperature difference (ΔT) over the length scale (h), which describes a box having a cold top and hot bottom surface such that liquid at the base is prone to rise. The importance of temperature changing over the length scale comes from the description of heat conduction of Fourier (1822). The classical formulation for bottom heating goes as h3 after all the various factors are combined (Rayleigh, 1916). The existing formulations for Earth’s Ra number with internal heating depend more strongly on the length scale, going as h5 (Schubert et al., 2001). Thus, previous geologic literature predicts that internal heating is more destabilizing than bottom heating. This is wrong, because internal heating warms the center of the box (Figure 1c). Thus, the middle is hotter than the bottom and is stable against convection. It is only the top half of the box that has a destabilizing temperature profile. The mathematical formula of Schubert et al. (2001) is apparently based on the destabilized upper half of an internally heated box.
Returning to material properties, at the time of Rayleigh, the kinetic theory of gas was fundamentally important to understanding how matter behaves. Then, and even recently, viscosity is viewed as diffusion of momentum. For a gas, this is indeed true because the diffusion of heat and mass are coupled indistinguishably. For a low density, small molecule liquid such as water, this is also reasonable but not exact because drag impedes motions in a liquid. High density fluids behave much differently: their viscosity depends on how strongly the material resists forces, as was known to Newton. The behavior of oil compared to honey during pouring provides evidence. Many quantitative studies exist of liquid foods, due to transport and storage needs (see the tables in our paper). Lyle’s Golden Syrup (which is similar to honey) is the most viscous substance that has been used to test the critical (minimum) Ra number (White, 1988). Compared to water (kinematic viscosity of 1 mm2s-1), syrup is a sluggish liquid (22,000 mm2s-1), but the mantle (~1021 mm2s-1) is far more viscous. The enormity of this extrapolation (17 order of magnitude) is paramount.
In mathematically comparing buoyancy to drag forces, via a dimensional analysis similar to that of Rayleigh, we conclude that convective instability for any material requires:
Ra > Sc = kinematic viscosity/mass self-diffusivity — (2)
where Sc is the Schmidt number. For water, the Schmidt number is ~1000, which is very similar to the critical Ra number of ~1700. The latter minimum value has been established from experiments on fluids in wide, flat boxes (h <= 10 mm), most of which have low viscosity. Regarding gas, it is well known that this state of matter convects under very low thermal gradients (the critical Ra of gas is ~1). Instability is consistent with gases actually diffusing momentum, so that the left side of (2) should equal unity. Sc = 1 is confirmed by experimental measurements of gas physical properties (Kestin et al., 1984).
For the mantle, mass diffusivities are minuscule but kinematic viscosities are immense. As a result the Schmidt number is ~1040. Thus, despite the immensity of Ra, convection is not expected. However, the tectonic plates on Earth’s surface do move, albeit at a pace of ~6 cm y-1, far slower than speed of a snail. Because it is well known that the heat source for mantle convection is inadequate, our current work is focused on what energy sources and forces may cause these sluggish motions.
References
-
Anderson, D.L., 2007. New Theory of the Earth, 2nd edition. Cambridge University Press, Cambridge.
-
Bercovici, D., 2015. Mantle Dynamics: An Introduction and Overview. In: Schubert, G., ed., Treatise on Geophysics. 7: 1-22.
-
Boresi A. P., Schmidt, R. J., 2003. Advanced Mechanics of Materials. John Wiley and Sons, Hoboken, NJ.
-
Fourier, J.B.J., 1822. Théorie Analytique de la Chaleur. Chez Firmin Didot, Paris. (translated in 1955 as The Analytic Theory of Heat (A. Freeman, Trans.). Dover Publications Inc., New York.
-
Kestin, J., Knierrim, K., Mason, E. A., Najafi, B., Ro, S. T., Waldman, M., 1984. Equilibrium and Transport Properties of the Noble Gases and their Mixtures at Low Density. Journal of Physical and Chemical Reference Data, 13: 229-303.
-
Kim, J.Y., Lee, K.B., Shin, Y.K., Bail, M.Y., Kim, B.Y., 2015. Changes in the rheological properties of cheddar cheese at different storage temperatures. Food Sci. and Biotech. 24, 1349-1353.
-
Luyten, H., 1988. The rheological and fracture properties of Gouda cheese. Ph.D. thesis, Laboratory of Dairying and Food Physics, Department of Food Science, Wageningen Agricultural University (223 pp).
-
Meyers, M. A., Chawla, K. K., 2009. Mechanical Behavior of Materials. Cambridge University Press, Cambridge.
-
Patterson, M. S., Weaver, C. W., 1970. Deformation of Polycrystalline MgO Under Pressure. Journal of the American Ceramic Society, 53: 463-471.
-
Rayleigh, L., 1916. On Convection Currents in a Horizontal Layer of Fluid When the Higher Temperature Is On the Underside. Philosophical Magazine, 32: 529-546.
-
Schubert, G., Turcotte, D. L., Olson, P., 2001. Mantle Convection in the Earth and Planets. Cambridge University Press, Cambridge.
-
White, D. B., 1988. The Planforms and Onset of Convection with a Temperature-Dependent Viscosity. Journal of Fluid Mechanics, 191: 247-286.
last updated 1st
June, 2019 |
