 |
Does subduction-induced mantle flow drive backarc extension? |
Zhihao Chen, Wouter P. Schellart, Vincent Strak, João C. Duarte
School of Earth, Atmosphere and Environment, Monash University, Melbourne, VIC 3800, Australia.
Corresponding author: zhihao.chen@monash.edu or zhchen11@gmail.com
Co-author emails: Wouter.Schellart@monash.edu ; Vincent.Strak@monash.edu ; Joao.Duarte@monash.edu
This webpage is a summary of: Chen, Z., W. P. Schellart, V. Strak and J. C. Duarte (2016), Does subduction-induced mantle flow drive backarc extension? Earth Planet. Sci. Lett., 441, 200-210, DOI: 10.1016/j.epsl.2016.02.027
Introduction
Subduction zones are one of the most striking feature on Earth. They represent one of the two types of convergent plate boundaries, in which one tectonic plates sinks underneath another into the Earth’s mantle. Soon after the advent of the theory of plate tectonics scientists recognized that subduction zones are one of the main drivers of plate motion and mantle convection [Elsasser, 1971]. With trench motion during progressive subduction, overriding plates incorporated in subduction zones may follow the trench and/or deform internally. Such deformation is often characterized by backarc extension, which leads to opening of backarc basins, such as the Tyrrhenian Sea, the Scotia Sea, the Aegean Sea, the North Fiji Basin, and the Lau Basin.
Mechanisms for backarc extension
A variety of mechanisms have been proposed to explain backarc extension. These include slab-rollback-induced trench suction at the subduction zone interface [e.g., Elsasser, 1971; Shemenda, 1993] and overriding plate collapse due to excess of potential energy [e.g., Hatzfeld et al., 1997; Gautier et al., 1999]. Other authors suggest there is a correspondence between backarc extension and subduction-induced mantle flow below the overriding plate, either in poloidal [Sleep & Toksöz, 1971] or toroidal fashion [e.g., Schellart & Moresi, 2013; Meyer & Schellart, 2013; Duarte et al., 2013; Sternai et al., 2014]. However, despite abundant attempts to explain the origin of backarc extension, the fundamental driving mechanism is still a matter of debate.
Mantle flow induced by subduction
Seismological and geochemical investigations suggest 3D subduction-induced mantle flow around lateral slab edges from the subslab zone towards the mantle wedge [e.g., Civello & Margheriti, 2004; Long & Silver, 2008; Diaz et al., 2010]. Such flow has also been observed in laboratory experiments [e.g., Buttles & Olson, 1998; Kincaid & Griffiths, 2003; Schellart, 2004; Funiciello et al., 2004; Strak & Schellart, 2014] and numerical models of subduction [e.g., Piromallo et al., 2006; Schellart et al., 2007; Jadamec & Billen, 2010; Faccenda & Capitanio, 2012; Schellart & Moresi, 2013]. It has been proposed that this flow is responsible for backarc extension [Schellart & Moresi, 2013; Duarte et al., 2013; Sternai et al., 2014]. In particular, using geodynamic numerical models of subduction, Schellart & Moresi [2013] presented quantitative results demonstrating that backarc extension at narrow subduction zones is driven by rollback-induced toroidal mantle flow. However, this driving mechanism has not been examined using physical laboratory models of subduction.
Feasibility with analogue modelling
In the last two centuries, analogue models have been used to study geological processes on the scale of metres to kilometres, such as folding and thrust-, normal-, and strike-slip faulting. In the last five decades, analogue models have also been designed to study large-scale geological processes such as subduction, orogenesis and rifting. The analogue modelling used to investigate the kinematics and dynamics of subduction has developed from 2D initially without an overriding plate [e.g., Jacoby, 1973; Shemenda, 1993] to 3D with or without an overriding plate [e.g., Kincaid & Olson, 1987; Funiciello et al., 2003; Schellart et al., 2004; Heuret et al., 2007; Sokoutis & Willingshofer, 2011; Meyer & Schellart, 2013; Duarte et al., 2013]. Earlier subduction models with an overriding plate used an external kinematic boundary condition imposed at the far-field edges of the subducting and/or overriding plate to maintain subduction [e.g., Shemenda, 1993; Heuret et al., 2007]. However, a challenge arises of how the imposed force/velocity can be properly scaled with respect to the internal forces/velocities of the system. To address this shortcoming a new modelling approach has been developed that includes a weak interplate material to lubricate the subduction zone interface to allow for low subduction zone interface coupling and progressive subduction [Meyer & Schellart, 2013; Duarte et al., 2013; Chen et al., 2015a].
Our models consist of two layers, following the setup of Duarte et al. [2013] and Meyer & Schellart [2013]. The top layer is made of a linear-viscous high-viscosity silicone mixed with fine iron powder, simulating a subducting plate (negative buoyant) and an overriding plate (neutrally buoyant). The lower layer is made of a linear-viscous low-viscosity glucose syrup to represent the sub-lithospheric upper mantle. An homogeneous lubricant mixture of petrolatum and paraffin is brushed on the top-surface of the subducting plate to obtain a low mechanical coupling at the subduction zone interface, following the procedure described in Duarte et al. [2013]. A stereoscopic Particle Image Velocimetry (sPIV) technique is introduced to map simultaneously overriding plate deformation and 3D subduction-induced mantle flow underneath and around an overriding plate, following an approach as described in Strak & Schellart [2014]. This improvement of the subduction analogue modelling and the use of the sPIV technique enable examination of the correlation between overriding plate deformation and subduction-induced mantle flow (Figure 1). Further details can be found in Chen et al. [2016].
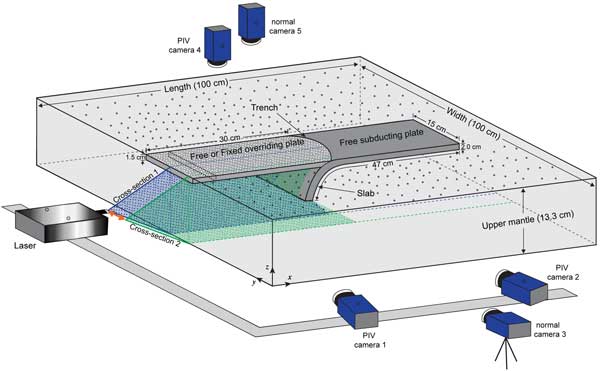
Figure 1: 3D configuration of the experimental setup. It includes a free high-viscosity subducting plate, a free/fixed high-viscosity overriding plate, a low-viscosity sub-lithospheric upper mantle and weak interplate mechanical coupling. The PIV system, consisting of a laser and three PIV high-resolution cameras, has been introduced to map progressive mantle flow simultaneously in stereo. For more detailed information, see Chen et al. [2016]. For enlargement of figure click here.
Conceptual model of backarc extension
With progressive subduction, the overriding plate experiences deformation that is characterized by localization of an area of maximum extensional strain within the interior of the plate at 6-10 cm (scaling to 300-500 km) from the trench (Figure 2a). We have observed forearc shortening for subduction models with a mobile overriding plate and forearc extension for those with a fixed overriding plate. We proposed that the style of forearc deformation (shortening and extension) is influenced by the mobility of the overriding plate through controlling the force normal to the subduction zone interface (trench suction). For detailed discussion see Chen et al. [2015b].
Our model results also showed that in the free sinking phase, the mantle material flows towards the mantle wedge in the upper half of the upper mantle, but in the opposite direction in the lower half (Figures 2b-2d). The mantle velocity in the upper half gradually increases trenchwards, and then rapidly decreases as it approaches the top surface of the slab. In the steady-state phase, the trenchward mantle flow in the upper half of the upper mantle is more pronounced than in the free sinking phase while the mantle flow in the lower half weakens.
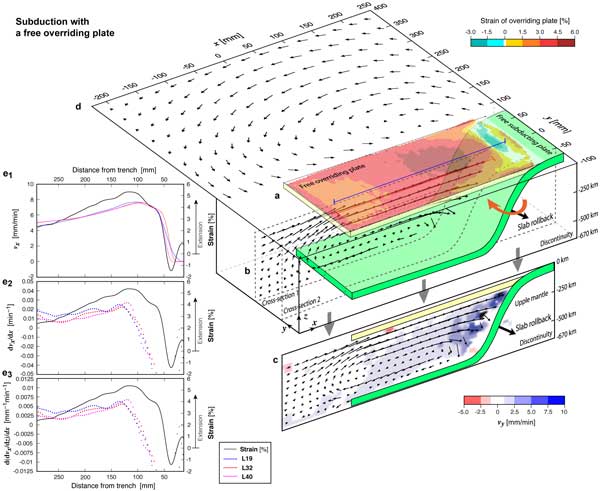
Figure 2: 3D scheme of overriding plate deformation and mantle flow in the dynamic laboratory model of narrow subduction with a free overriding plate. (a) Strain map of overriding plate deformation; (b) Velocity field in the central cross-section; (c) Velocity field in the lateral edge cross-section; (d) Surface velocity field; (e) correction between the overriding plate strain and the trench normal horizontal mantle velocity (vx), corresponding trench-normal horizontal mantle velocity gradient (dvx/dx) and trench-normal horizontal gradient of the vertical mantle velocity gradient (d(dvx/dz)/dx) at 3-5 cm (scaling to 15-25 km) below the base of the overriding plate, respectively. For more detailed information see Chen et al. [2016]. For enlargement of figure click here.
In order to determine the relationship between overriding plate deformation and subduction-induced mantle flow, we quantify and compare both when subduction reaches a steady-state phase. We select this period to calculate their correlation because at this time subduction is characterized by comparable subduction kinematics (trench velocity and subducting plate velocity) and comparable mantle flow patterns. Our results show a comparable position of the maximum trench-normal gradient of the sub-lithospheric vertical mantle velocity gradient (d(dvx/dz)/dx) underneath the plate and the maximum trench-normal extensional strain in the overriding plate (within 0-2 cm of each other) (Figure 2e). This comparison demonstrates a direct link between subduction-induced mantle flow and overriding plate deformation, where rollback-induced mantle flow creates a trench-normal horizontal velocity gradient below the overriding plate that induces a shear drag gradient at the base of the overriding plate that drives its extension. Our further analysis indicates that the toroidal component of mantle flow has a larger contribution to overriding plate deformation than the poloidal component.
We also estimated stresses in the overriding plate to examine the role of trench suction in the deformation of the overriding plate. Calculations based on our models indicate that the tensional horizontal trench-normal deviatoric stress in the backarc region (scaling to ~28.8 MPa) induced by basal drag is about 8-12 times larger than the trench-normal stress resulting from the horizontal component of the trench suction force (scaling to ~2.4-3.6 MPa).
The model results provide direct support that subduction-induced mantle flow (predominantly toroidal) is responsible for backarc extension. This mechanism can explain backarc extension at narrow subduction zones such as the Alboran basin at Gibraltar, the Tyrrhenian Sea at Calabria, the Aegean Sea behind the Hellenic arc and the Scotia Sea. Besides narrow subduction zones, our results also have an application to wider subduction zones such as the Melanesian system and the Northwest Pacific system. Their edge segments are characterized by backarc extension as well. We infer that the edges of wider subduction zones are also characterized by toroidal mantle flow driven by the retreating edge segments of wider slabs. Such mantle flow could drive backarc extension at the edge segments of wider subduction zones.
References
-
Buttles, J., and P. Olson (1998), A laboratory model of subduction zone anisotropy, Earth Planet. Sci. Lett., 164, 245-262.
-
Chen, Z., W. P. Schellart, and J. C. Duarte (2015a), Quantifying the energy dissipation of overriding plate deformation in three-dimensional subduction models, J. Geophys. Res., Solid Earth, 120, 519-536, doi:10.1002/2014JB011419.
-
Chen, Z., W. P. Schellart, and J. C. Duarte (2015b), Overriding plate deformation and variability of fore-arc deformation during subduction: insight from geodynamic models and application to the Calabria subduction zone. Geochem. Geophys. Geosyst., 16, 3697-3715, doi:10.1002/2015GC005958.
-
-
Civello, S., and L. Margheriti (2004), Toroidal mantle flow around the Calabrian slab (Italy) from SKS splitting, Geophys. Res. Lett., 31, doi:10.1029/2004GL019607.
-
Diaz, J., J. Gallart, A. Villasenor, F. Mancilla, A. Pazos, D. Cordoba, J. A. Pulgar, P. Ibarra, and M. Harnafi (2010), Mantle dynamics beneath the Gibraltar Arc (western Mediterranean) from shear-wave splitting measurements on a dense seismic array, Geophys. Res. Lett., 37, L18304, doi:10.1029/2010GL044201.
-
Duarte, J. C., W. P. Schellart, and A. R. Cruden (2013), Three-dimensional dynamic laboratory models of subduction with an overriding plate and variable interplate rheology, Geophy. J. Int., 195, 47-66.
-
Elsasser, W. M. (1971), Sea-floor spreading as thermal convection, J. Geophys. Res., 76, 1101-1112.
-
Faccenda, M., and F. A. Capitanio (2013), Seismic anisotropy around subduction zones: Insights from three-dimensional modeling of upper mantle deformation and SKS splitting calculations, Geochem. Geophys. Geosyst., 14, 243-262.
-
Funiciello, F., C. Faccenna, and D. Giardini (2004), Role of lateral mantle flow in the evolution of subduction systems: insights from laboratory experiments, Geophy. J. Int., 157, 1393-1406.
-
Gautier, P., J.-P. Brun, R. Moriceau, D. Sokoutis, J. Martinod, and L. Jolivet (1999), Timing, kinematics and cause of Aegean extension: a scenario based on a comparison with simple analogue experiments, Tectonophysics, 315, 31-72.
-
Hatzfeld, D., J. Martinod, G. Bastet, and P. Gautier (1997), An analog experiment for the Aegean to describe the contribution of gravitational potential energy, J. Geophys. Res., Solid Earth, 102, 649-659.
-
Heuret, A., F. Funiciello, C. Faccenna, and S. Lallemand (2007), Plate kinematics, slab shape and back-arc stress: A comparison between laboratory models and current subduction zones, Earth Planet. Sci. Lett., 256, 473-483.
-
Jacoby, W. R. (1973), Model experiment of plate movements, Nat. Phys. Sci., 242, 130-134.
Jadamec, M. A., and M. I. Billen (2010), Reconciling surface plate motions with rapid three-dimensional mantle flow around a slab edge, Nature, 465, 338-342.
-
Kincaid, C., and P. Olson (1987), An experimental study of subduction and slab migration, J. Geophys. Res., 92, 13832-13840.
-
Kincaid, C., and R. W. Griffiths (2003), Laboratory models of the thermal evolution of the mantle during rollback subduction, Nature, 425, 58-62.
-
Long, M. D., and P. G. Silver (2008), The subduction zone flow field from seismic anisotropy: A global view, Science, 319, 315-318.
-
Meyer, C., and W. P. Schellart (2013), Three-dimensional dynamic models of subducting plate-overriding plate-upper mantle interaction, J. Geophys. Res., Solid Earth, 118, 775-790.
-
Piromallo, C., T. W. Becker, F. Funiciello, and C. Faccenna (2006), Three-dimensional instantaneous mantle flow induced by subduction, Geophys. Res. Lett., 33, L08304, doi:10.1029/2005GL025390.
-
Schellart, W. P. (2004), Kinematics of subduction and subduction-induced flow in the upper mantle, J. Geophys. Res., Solid Earth, 109, B07401, doi:10.1029/2004JB002970.
-
Schellart, W. P., J. Freeman, D. R. Stegman, L. Moresi, and D. May (2007), Evolution and diversity of subduction zones controlled by slab width, Nature, 446, 308-311.
-
Schellart, W. P., and L. Moresi (2013), A new driving mechanism for backarc extension and backarc shortening through slab sinking induced toroidal and poloidal mantle flow: Results from dynamic subduction models with an overriding plate, J. Geophys. Res., Solid Earth, 118, 3221-3248.
-
Shemenda, A. I. (1993), Subduction of the lithosphere and back arc dynamics: Insights from physical modeling, J. Geophys. Res., Solid Earth, 98, 16167-16185.
-
Sleep, N., and M. N. Toksöz (1971), Evolution of marginal basins, Nature, 233, 548-550.
Sokoutis, D., and E. Willingshofer (2011), Decoupling during continental collision and intra-plate deformation, Earth Planet. Sci. Lett., 305, 435-444.
-
Sternai, P., L. Jolivet, A. Menant, and T. Gerya (2014), Driving the upper plate surface deformation by slab rollback and mantle flow, Earth Planet. Sci. Lett., 405, 110-118.
-
Strak, V., and W. P. Schellart (2014), Evolution of 3-D subduction-induced mantle flow around lateral slab edges in analogue models of free subduction analysed by stereoscopic particle image velocimetry technique, Earth Planet. Sci. Lett., 403, 368-379.
last updated 4th September, 2016 |
