 |
The Effect of Water
in the Depleted Mantle
on the
660-km Seismic Discontinuity
|
Sujoy Ghosh1,2, Eiji Ohtani1, Konstantin D. Litasov1,3,4, Akio Suzuki1, David Dobson5, Kenichi Funakoshi6
1Department of Earth and Planetary Material Science, Tohoku University, Sendai 980-8578, Japan, sujoy.ghosh@erdw.ethz.ch ; ohtani@m.tohoku.ac.jp ; klitasov@yahoo.com ; a-suzuki@m.tohoku.ac.jp
2Institute of Geochemistry and Petrology, ETH Zürich, CH-8092, Zürich, Switzerland
3Novosibirsk State University, Novosibirsk, 630090, Russia
4V.S. Sobolev Institute of Geology and Mineralogy SB RAS, 630090, Russia
5Department of Earth Sciences, University College London, Gower Street, London WC1E 6BT, UK, d.dobson@ucl.ac.uk
6SPring-8, Japan Synchrotron Radiation Research Institute, Kouto, Japan, funakosi@spring8.or.jp
This webpage is a summary of: Ghosh, Sujoy, Eiji Ohtani, Konstantin D. Litasov, Akio Suzuki, David Dobson, Kenichi Funakoshi, 2013, Effect of water in depleted mantle on post-spinel transition and implication for 660 km seismic discontinuity, Earth and Planetary Science Letters, 371–372, 103–111.
Introduction
The 660-km discontinuity is one of the most important structural boundaries in the Earth's interior. It has been widely accepted to be due to a phase transition in the (Mg,Fe)2SiO4 system. At this boundary (Mg,Fe)2SiO4 (γ-spinel or ringwoodite) transforms to a mixture of (Mg,Fe)SiO3 (Mg-perovskite) and (Mg,Fe)O (ferropericlase). According to seismic observations the boundary occurs at a depth corresponding to a pressure of about 23.6 GPa at 1873 K (Dziewonski & Anderson, 1981). This phase boundary is endothermic (Christensen, 1995) and is often called the post-spinel transition. The 660-km discontinuity is a global feature, but seismological studies suggest that its depth varies considerably in different regions (e.g., Flanagan & Shearer, 1998; Helffrich, 2000; Gu & Dziewonski, 2002). The most often mentioned effect to explain these seismic observations is the lateral variation or gradient in temperature (e.g., Shearer, 2000) beneath 660-km (Helffrich, 2000). Only a few studies evoke chemical changes as well (e.g., Cornwell et al., 2011).
In situ X-ray diffraction measurements have been made on pure Mg2SiO4 (Irifune et al., 1998; Katsura et al., 2003; Fei et al., 2004a) and a pyrolitic composition (Litasov et al., 2005a) using the multi-anvil technique. The results suggest that the boundary occurs at pressures lower than the actual pressure at 660 km (23.6 GPa) and that a gentle negative Clapeyron slope ranges from −0.4 to −1.3 MPa/K (e.g., Katsura et al., 2003; Fei et al., 2004a; Litasov et al., 2005a). As a result, large variations in the depth of 660-km discontinuity cannot be explained by a temperature effect only.
In our study we re-examine the post-spinel transition boundary in Mg2SiO4 and present new data in Mg2SiO4 + 2 wt.% H2O by means of in situ X-ray diffraction in a multi-anvil apparatus at SPring-8, Japan, the world’s largest third-generation synchrotron radiation facility. Our data show the influence of water on the post-spinel transition and we interpret the results in terms of the 660-km seismic discontinuity and variations in its depth.
Comparison of our results with others
We compared our results with previous studies on Mg2SiO4, (Mg,Fe)2SiO4 and pyrolite compositions (Figure 1). Several methods have been used to study the transition of the post-spinel boundary. These include quench laboratory experiments using multi-anvil apparatus (e.g., Ito & Takahashi, 1989; Ishii et al., 2011), thermodynamic and theoretical calculations (e.g., Akaogi et al., 1989; Yu et al., 2007), in situ X-ray diffraction measurements using the multi-anvil technique (e.g., Irifune et. al., 1998; Katsura et al., 2003; Fei et al., 2004a) and in situ LHDAC (Laser Heated Diamond Anvil Cell) experiments (e.g., Chudinovskikh & Boehler, 2001; Shim et al., 2001). In all these cases, the measured and calculated boundaries of the post-spinel transition in Mg2SiO4 were located from 21 to 23.5 GPa and at 1500-1900 K.
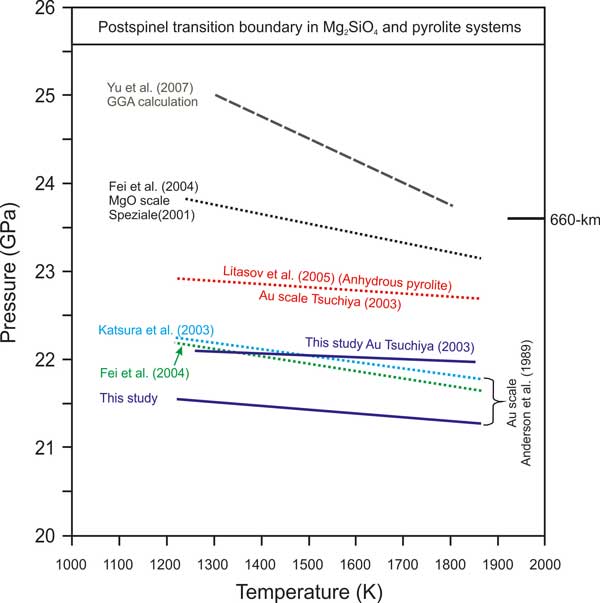
Figure 1: The post-spinel transition boundary in Mg2SiO4 using the Au pressure scale (Tsuchiya et al. 2001) in this study (blue solid line), along with previous results in Mg2SiO4 and pyrolite systems using different pressure scales. At the bottom, the post-spinel transition in Mg2SiO4 in this study (blue solid line) is compared with previous results [Katsura et al., 2003 (blue dashed line); Fei et al., 2004a (green dashed line) in the Au scale by Anderson et al., 1989]. The post-spinel transition boundary in Mg2SiO4 using the MgO scale (Speziale et al., 2001) by Fei et al. (2004a; grey dashed line) and using the GGA calculation by Yu et al. (2007; black dashed line) is also plotted. The post-spinel transition boundary is plotted in the pyrolite composition using the Au scale (Tsuchiya et al., 2001) by Litasov et al. (2005a; red dashed line).
Using a Fo90 composition and the quench technique in a multi-anvil apparatus, Ito & Takahashi (1989) located the post-spinel transition boundary at 23 GPa and 1900 K with a steep Clapeyron slope of -3.0 MPa/K. The first in situ measurements by Irifune et al. (1998) for this boundary in Mg2SiO4 using the Au pressure scale (Anderson et al., 1989) found essentially the same negative Clapeyron slope as observed by Ito & Takahashi (1989). Since they used the Au pressure scale (Anderson, 1989), the phase boundary was placed at a pressure of more than 2 GPa lower than occurs at the 660-km discontinuity. Later LHDAC experiments and improved techniques in the multi-anvil press have confirmed that this boundary occurs at higher pressures (Chudinovskikh & Boehler, 2001; Shim et al., 2001; Katsura et al., 2003; Fei et al., 2004a).
Katsura et al. (2003) showed that the post-spinel transition is very sluggish, so that complete transformation from Rw to Pv and Pc is difficult, especially at high temperature (~2000 K). The phase boundary of the post-spinel transition determined in the present study using the Au scale by Tsuchiya (2003) is at a slightly lower (~0.3-0.5 GPa) pressure than that of Katsura et al. (2003) and Fei et al. (2004a), recalculated to the same pressure scale. This minor discrepancy is almost inside the possible uncertainties and may be explained by differences in cell assembly configurations. Fei et al. (2004b) have discussed the accuracy of the different pressure scales and observed that the MgO pressure scale (Speaziale et al., 2001) may be more reliable compared to Au, Pt and NaCl. It places the post-spinel transition boundary in Mg2SiO4 at 23.6 GPa at 1673 K, which is close to the pressure of 660-km discontinuity. In the present study the transition pressure based on the Au pressure scale by Tsuchiya (2003) is about 1.5 GPa lower than the pressure at 660 km (Figure 1).
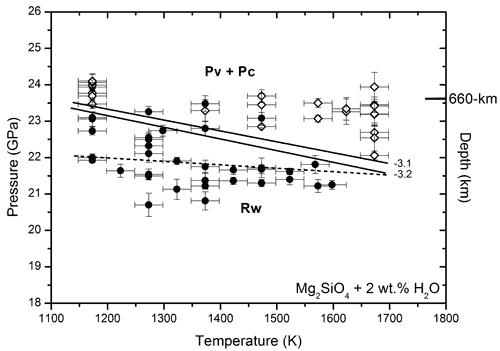
Figure 2: Phase diagram of Mg2SiO4 + 2 wt.% H2O based on the Au pressure scale by Tsuchiya (2003). The solid black circles and solid white diamonds represent data points indicating increase of Ringwoodite (Rw) and/or decrease of Perovskite+Periclase (Pv+Pc) and decrease of Rw and/or increase of Pv+Pc, respectively. The solid black lines are the upper and lower boundaries of the Post-spinel transition (PST) boundary in hydrous Mg2SiO4 with the Clapeyron slope between -3.2 and -3.1 MPa/K. The PST boundary in Mg2SiO4 determined in this study (Au pressure scale by Tsuchiya (2003); dashed line) is plotted for comparison.
Our experimental data suggest that the shift of the 660-km discontinuity resulting from adding water can be up to 1.3 GPa, corresponding to an increase in depth of 40 km. The Clapeyron slope found in the present study in Mg2SiO4 is much gentler than the theoretical value (Yu et al., 2007) and the results from quench experiments (Ito & Takahashi, 1989). However, we found the same gentle Clapeyron slope in the present study as previous in situ studies in Mg2SiO4 (Katsura et al., 2003; Fei et al., 2004a). The quench experiments by Ito & Takahashi (1989) found a Clapeyron slope of −3.0 MPa/K, which is significantly smaller than those obtained by recent in situ X-ray diffraction experiments (this study: from −0.04 to −0.85 MPa/K; Katsura et al. (2003): from −2.0 to −0.4 MPa/K; Fei et al. (2004a); −1.3 MPa/K; Litasov et al. (2005a): from −0.8 to −0.2 MPa/K). In the present study, we constrain the upper and lower boundaries of the Clapeyron slope in Mg2SiO4 + 2 wt.% H2O to lie between −3.2 and −3.1 MPa/K. In contrast to the in situ studies of anhydrous systems, the Clapeyron slope of the PST in water-bearing Mg2SiO4 and pyrolite is significantly steeper from −3.2 to −3.1 MPa/K in Mg2SiO4 in the present work and −2.2 MPa/K in hydrous pyrolite (Litasov et al., 2005b).
Summary
Our data suggest that water has a strong influence on 660-km discontinuity. The depressions observed at this boundary in several regions, especially subduction zones, can be explained by the presence of water in the depleted harzburgite component.
References
-
Akaogi, M., Ito, E., and Navrotsky, A., 1989, Olivine-modified spinel–spinel transition in the system Mg2SiO4–Fe2SiO4 calorimetric measurements, thermochemical calculation, and geophysical application, J. Geophys. Res., 94, 15671-15685.
-
Anderson, O.L., Issak, D.G., Yamamoto, S., 1989, Anharmonicity and the equation of state for gold, J. Appl. Phys., 65, 1534-1543.
-
Christensen, U.R., 1995. Effects of phase transitions on mantle convection, Annu. Rev. Earth Planet. Sci., 23, 65–87.
-
Chudinovskikh, L., Boehler, R., 2001, High-pressure polymorphs of olivine and the 660-km seismic discontinuity, Nature, 411, 574-577.
-
Cornwell, D.G., Hetényi, G. and Blanchard T.D., 2011, Mantle transition zone variations beneath the Ethiopian rift and Afar: Chemical heterogeneity within a hot mantle?, Geophys. Res. Lett., 38, L16308, doi:10.1029/2011GL047575
-
Dziewonski, A.M., Anderson, D.L., 1981, Preliminary reference Earth model, Phys. Earth Planet. Inter., 25, 297-356.
-
Fei, Y., J. Li, K. Hirose, W. Minarik, J. Van Orman, C. Sanloup, W. van Westrenen, T. Komabayashi, K. Funakoshi, 2004b, A critical evaluation of pressure scales at high temperatures by in situ X-ray diffraction measurements, Phys. Earth Planet Inter., 143/144, 516-526.
-
Fei, Y., Van Orman, J., Li, J., van Westrenen, W., Sanloup, C., Minarik, W., Hirose, K., Komabayashi, T., Walter, M., and Funakoshi, K., 2004a, Experimentally determined postspinel transformation boundary in Mg2SiO4 using MgO as an internal pressure standard and its geophysical implications, J. Geophys. Res., 109, doi: 10.1029/2003JB002562.
-
Flanagan, M.P., Shearer, P.M., 1998, Global mapping of topography on transition zone velocity discontinuities by stacking SS precursors, J. Geophys. Res., 103, 2673-2692.
-
Ghosh, Sujoy, Eiji Ohtani, Konstantin D. Litasov, Akio Suzuki, David Dobson, Kenichi Funakoshi, 2013, Effect of water in depleted mantle on post-spinel transition and implication for 660 km seismic discontinuity, Earth and Planetary Science Letters, 371–372, 103–111.
-
Gu, Y.J., Dziewonski, A.M., 2002, Global variability of transition zone thickness, J. Geophys. Res., 107, doi: 10/1029/2001JB000489.
-
Helffrich, G.R., 2000, Topography of the transition zone seismic discontinuities, Rev. Geophys., 38, 141-158.
-
Irifune, T., Nishiyama, N., Kuroda, K., Inoue, T., Isshiki, M., Utsumi, W., Funakoshi, K., Urakawa, S., Uchida, T., Katsura, T., Ohtaka, O., 1998, The postspinel phase boundary in Mg2SiO4 determined by in situ X-ray diffraction, Science, 279, 1698-1700.
-
Ishii, T., Kojitani, H., Akaogi, M., Post-spinel transitions in pyrolite and Mg2SiO4 and akimotoite-perovskite transition in MgSiO3: Precise comparison by high-pressure high-temperature experiments with multi-sample cell technique, Earth Planet. Sci. Lett., 309, 185-197, 2011.
-
Ito, E., and Takahashi, E. 1989, Post-spinel transformation in the system Mg2SiO4–Fe2SiO4 and some geophysical implications, J. Geophys. Res., 94, 10637-10646.
-
Katsura, T., Yamada, H., Shinmei, T., Kubo, A., Ono, S., Kanzaki, M., Yoneda, A., Walter, M.J., Ito, E., Urakawa, S., Funakoshi, K., and Utsumi, W., 2003, Post-spinel transition in Mg2SiO4 determined by high P-T in situ X-ray diffraction, Phys. Earth Planet. Inter., 136, 11-24.
-
Litasov, K.D., Ohtani, E., Sano, A., Suzuki, A., and Funakoshi, K., 2005a, In situ X-ray diffraction study of post-spinel transformation in a peridotite mantle: Implication to the 660-km discontinuity, Earth Planet. Sci. Lett., 238, 311-328.
-
Litasov, K.D., Ohtani, E., Sano, A., Suzuki, A., and Funakoshi, K., 2005b, Wet subduction versus cold subduction, Geophys. Res. Lett., 32, L13312, doi:10.1029/2005GL022921.
-
Shearer P.M., 2000, Upper mantle seismic discontinuities, Earth’s deep interior: Mineral physics and tomography from the atomic to global scale, American Geophysical Union, Geophysical Monograph, 117, 115-131.
-
Shim, S.H., Duffy, T.S., Shen, G., 2001, The post-spinel transformation in Mg2SiO4 and its relation to the 660-km seismic discontinuity, Nature, 411, 571-574.
-
Speziale, S., Zha, C.S., Duffy, T.S., Hemley, R.J., Mao, H.K., 2001, Quasi-hydrostatic compression of magnesium oxide to 52 GPa: implications for the pressure-volume-temperature equation of state, J. Geophys. Res., 106, 515-528.
-
Tsuchiya, T., 2003, First-principles prediction of the P–V–T equation of state of gold and the 660-km discontinuity in Earth’s mantle, J. Geophys. Res., 108, doi:10.1029/2003JB002446.
-
Yu, Y.G., Wentzcovitch, R.M., Tsuchiya, T., Umemoto, K., Weidner, D.J., 2007, First principles investigation of the postspinel transition in Mg2SiO4, Geophys. Res. Lett., 34, doi: 10.1029/2007GL029462.
last updated 18th November, 2013 |
