Heat Transport in Melts, Minerals, Glasses, and Rocks: Implications for Magma Genesis

Anne M. Hofmeister¹, Alan G. Whittington² & Peter I. Nabelek²

¹Department of Earth and Planetary Sciences, Washington University, St. Louis, MO, 63130 USA, hofmeist@levee.wustl.edu

²Department of Geological Sciences, University of Missouri, Columbia, MO, USA, whittingtona@missouri.edu ; nabelekp@missouri.edu

This webpage is a synopsis of the paper: Whittington, A.G., A.M. Hofmeister & P.I. Nabelek, Temperature-dependent thermal diffusivity of the Earth’s crust and implications for magmatism, Nature, 458, 319-321, 2009, doi:10.1038/nature07818.

For News & Views comment, click here.

Summary

Magmatic processes are dynamic, so understanding and modeling these complex events requires data on the thermal transport properties of not only the surrounding terrain, but also of the melts themselves. Recent advances in laser-flash analysis permit accurate measurement of thermal diffusivity (D) of Earth materials as a function of temperature (T). They show that D decreases more strongly with T than previously thought. Moreover, D decreases, sometimes drastically, from crystal to glass to melt of the same composition. Both aspects of thermal diffusivity are conducive to melting. For example, our recent thermal model of continental collisions indicates that D depending on T enhances the impacts of strain heating or of radiogenic emissions in producing deep crustal melts.

Introduction

The response of a material to applied heat depends on its physical properties, such as the melting temperature. How fast heat travels through any given material is particularly important because materials that transport heat slowly stay warm for longer periods. Thermal history is governed by the physical property thermal conductivity (k) through Fourier’s equations.

Earth materials are generally opaque in appearance. However, our eyes sense the visible, rather than the near-infrared spectral region, which is the energy region associated with geologic temperatures. Rocks, minerals and their glasses and melts are transparent in the near-IR, even if colored, e.g., by Fe ions. Because of these spectral characteristics, laboratory measurements of heat flow involve some portion of the applied heat being carried from the heater across the material to the sensor by light (photons) and some portion being moved from atom-to-atom within the solid via vibrations (phonons; Figure 1). Photon transfer in the laboratory is not a diffusional process, as a material need not even be present. In most experiments, no means exists to differentiate whether the sensor (generally a thermocouple) is heated by phonons diffusing or photons hopping across the sample (see summary in Hofmeister et al., 2007).

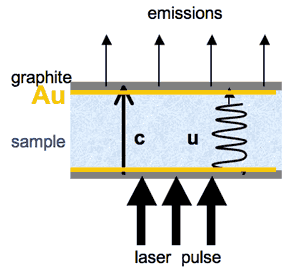
Figure 1: Schematic of heat transfer in a material that is transparent over some spectral region. A sample disk (blue stipple with coated top and bottom) of thickness L is held at temperature by the furnace. Emissions from the top of the sample (light arrows) are monitored by an IR detector, providing a baseline, which is set to null intensity for convenience (Figure 2). A laser pulse (heavy arrows) heats the coated bottom of the sample.

Technology Transfer

Laser-Flash Analysis (LFA, Parker et al., 1961) is the industry standard for measuring thermal diffusivity (D) which is the rate at which cooling occurs and is closely related to thermal conductivity. Because k = ρC_PD, where ρ is density and C_P is heat capacity, and these later properties are easily measured or calculated, LFA measurements provide the key variable needed to quantify heat transport.

In LFA, heat flow across a sample is recorded as a function of time (Figure 2). Arrival times of the photons and phonons are easily distinguished because of a factor of 100,000 difference in speeds. The need to constrain heat transport in glasses and other highly transparent optical materials for applications in engineering and materials science motivated development of mathematical models (Mehling et al., 1998) that quantitatively remove spurious radiative transfer effects. Metal and graphite coatings are also used to reduce photon flux (Degiovanni et al., 1994). These recent advances permit accurate measurement of thermal diffusivity for rocks, minerals, glasses and melts. The technique has additional advantages in studying geologic materials such as being contact free and quantifying orientational differences (Hofmeister et al., 2007).

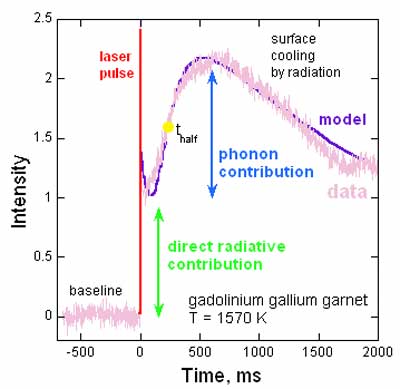
Figure 2. Time-temperature curves in LFA. Measured emissions = pink. The immediate rise after the laser pulse (red) is due to direct radiative transfer (green). Diffusion of heat by vibrations provides a slower rise (blue) and can be estimated from the half rise time (yellow dot). Emissions increase to a maximum, and then the sample radiates heat to the surroundings until equilibrium is again attained. Purple = the mathematical model of Mehling et al. (1998) which accounts for both processes. After Hofmeister (2006).

Results

Systematic LFA studies have been made of several common rock-forming mineral families, structural analogues for high-pressure phases, and various glasses, melts, and rocks (e.g., Hofmeister, 2006; Perterman et al., 2008; Whittington et al., 2009). Our results are sufficiently accurate to reveal phase transitions and distinguish between the effects of grain size and porosity (Branlund & Hofmeister, 2008). We have found that previous methods underestimated D at 298 K due to contact losses by 10% per thermal contact, but at high temperature D has been seriously overestimated, sometimes by a factor of 5 (Perterman & Hofmeister, 2006; Branlund & Hofmeister, 2007; Hofmeister et al., 2007).

Nowhere are the strongly insulating properties of geologic materials more evident than in our measurements of glasses and melts (Figure 3). We have found that isochemical melting reduces the thermal diffusivity by a non-trivial amount for felsic minerals and rocks (Perterman et al., 2008; Whittington et al., 2009) whereas isochemical melting in mafic rocks drastically reduces D (Hofmeister et al., 2009).

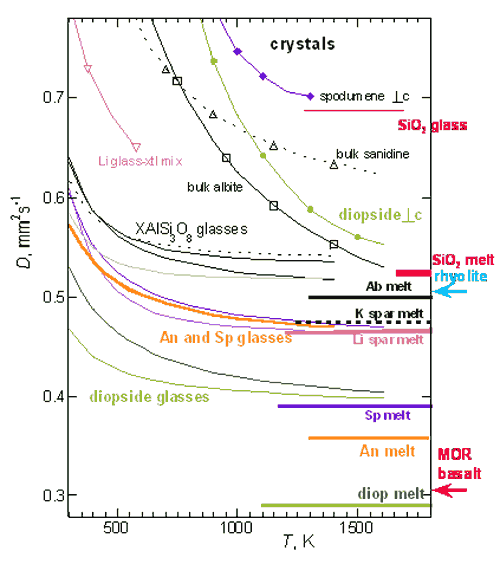
Figure 3. Comparison of thermal diffusivities. Melts shown as thick lines, glasses as thin lines, and crystals as very fine lines with symbols. Compositions are as labeled and the same type (or color) of line was used for all three states. Spodumene = purple. Diopside = green. Li-feldspar = light pink. K-feldspar = black, widely spaced dots. Albite = black, solid. Anorthite = orange. Remelts of diopside and albite are shown as darker colors. Crystals in the Li mixture are spodumene, due to incongruent melting. Silica = hot pink (Hofmeister, Branlund and Whittington, in prep.) Rhyolite (Romine, 2008) and basalt (Galenas et al., 2008) studies are ongoing. Modified from Hofmeister et al. (2009).

Companion measurements of viscosity (Hofmeister et al., 2009) complete the picture of the transport properties of melts. We have found that the two properties are related through the configurational changes (see discussion of heat capacity, e.g., Richet & Bottinger, 1995). Observation of systematic behavior in the feldspar and pyroxene systems allows us to estimate D for real magmas (Figure 3). Current studies of natural basaltic and rhyolitic lavas (Romine, 2008; Galenas et al., 2008) support the estimates.

Implications

Because previous data on D (or k) did not reveal the large difference between low and high temperature heat transport, constant values have largely been used in models of heat flow, whether conduction or convection is involved. Consequently, the insulating nature of hot rocks has been seriously underestimated whereas cold rocks have been considered to retain much more heat than is truly possible (see discussions by Yuen et al., 2000 and Braun, 2009).

The effect of the variable D on the thermal evolution of the continental lithosphere was examined in a thermal model of continental collision (Whittington et al., 2009) that builds on previous models based on constant D (e.g., Nabelek and Liu, 2004). We found that strain heating in the shear zones was trapped by the highly insulating rock, and that crustal melting does not require extraordinary high levels of radioactivity. The thermal properties of the rocks and positive feedback led to generation of leucogranite melts in the Himalayas and other collisional orogens. Our model does not include the enhanced insulation provided once melt is formed. For the case studied, the rocks at high T alone provide enough insulation to reach melting temperatures, given the presence of strain heating. For continental hot spots, the need for a long-term flux of mafic magma to produce the observed quantities of silicic magma (Annen & Sparks, 2002; Annen et al., 2006) should be reduced when the low thermal diffusivity of hot crust is taken into account.

Our data on feldspar and pyroxene crystals, glasses and melts (Figure 3; Hofmeister et al., 2009) point to mafic systems undergoing more dramatic changes in thermal properties on melting. For this case, the difference of rock and melt is key because at mantle temperatures, D is more or less independent of temperature. Once partial melting commences, heat transport by conduction is impeded. This represents a positive feedback effect, because heat retention will increase the melt fraction which in turn further decreases thermal diffusivity and conductivity of the melting zone. The very large difference in D between pyroxenes and their melts (and anorthite and its melt), which proxy for mafic systems (Figure 3) may contribute to the large melt fractions that are associated with production of basaltic magma. Large melt fractions are also more easily mobilized and extracted, processes that are also promoted by the low viscosity of basalts. The different styles of felsic and mafic magmatism are tied in part to contrasting behavior in both transport properties (D and viscosity).

What does this mean for plumes?

We suggest that for the oceanic lithosphere, which is near solidus everywhere at its base, a small perturbation in the system will produce magmatism connected with ridges and hot spots. Huge amounts of heat carried from the core-mantle boundary are probably not needed to produce longevity in basaltic magmatism or its huge volumes, due to thermal feedback provided by exceedingly insulating melts. Several possibilities come to mind: the heat could come from the upwellings in an upper mantle circulation system, or geotherms in the upper mantle system being slightly uplifted by upwellings in lower mantle circulation (see patterns in Hofmeister & Criss, 2005). For hot spots such as Iceland, lower solidus temperatures associated with chemical heterogeneities in the upper mantle, may provide a nudge. Hydration alone reduces thermal diffusivity (Hofmeister et al., 2006). Additional measurements and thermal models are needed to test these hypotheses.

References

• Annen C and Sparks RSJ (2002) Effects of repetitive emplacement of basaltic intrusions on thermal evolution and melt generation in the crust. Earth and Planetary Science Letters, 203, 937-955.
• Annen C, Blundy JD and Sparks RSJ (2006) The genesis of intermediate and silicic magmas in deep crustal hot zones. Journal of Petrology, 47, 505-539.
• Branlund J.M. and Hofmeister A.M. (2007) Thermal diffusivity of quartz to 1000 degrees C: Effects of impurities and the a-b phase transition. Phys. Chem. Minerals, 34, 581-595.
• Branlund J.M. and Hofmeister A.M. (2008) Factors affecting heat transfer in SiO₂ solids. American Mineralogist, 93, 1620-1629.
• Braun, J. (2009) Hot blanket in Earth’s deep crust. Nature, 458, 292-293.
• Degiovanni A Andre S Maillet D (1994) Phonic conductivity measurement of a semi-transparent material. In: Tong TW (ed) Thermal conductivity 22. Technomic, Lancaster, PN, pp 623-633.
• Galenas, M.G., Whittington, A., and Hofmeister, A., 2008. Transport Properties of Mid-ocean Ridge Basalt from the East Pacific Rise. IAVCEI 2008 General Assembly, Reykjavik, Iceland.
• Hofmeister, A.M. (2006) Thermal diffusivity of garnets to high temperature. Physics and Chemistry of Minerals, 33, 45-62.
• Hofmeister, A.M and Criss, R.E. (2005) Mantle convection and heat flow in the triaxial Earth. In: Plates, Plumes, and Planetary Processes, edited by G. R. Foulger, J.H. Natland, D.C. Presnall, and D.L. Anderson, Geological Society of America Special Paper 388, pp 289-302.
• Hofmeister A.M., Pertermann, M., Branlund, J. and Whittington, A.G. (2006) Geophysical implications of reduction in thermal conductivity due to hydration. Geophysical Research Letters, 33,  doi: 10.1029/2006GL026036.
• Hofmeister, A.M., Pertermann, M. and Branlund, J. M. (2007) Thermal conductivity of the Earth. Treatise in Geophysics, G. Schubert, Ed. In Chief, V. 2 Mineral Physics, G.D. Price, ed. Elsevier, The Netherlands, pp 543-578.
• Hofmeister A.M., Whittington A.G., and Pertermann, M. (2009) Transport properties of high albite crystals and near-endmember feldspar and pyroxene glasses and melts to high temperature. Contributions to Mineralogy and Petrology, doi: 10.1007/s00410-009-0388-3.
• Mehling H Hautzinger G Nilsson O Fricke J Hofmann R Hahn O (1998) Thermal diffusivity of semitransparent materials determined by the laser-flash method applying a new mathematical model. Internatl. J Thermophys. 19, 941-949.
• Nabelek, P. I., and Liu, M., 2004, Petrologic and thermal constraints on the origin of leucogranites in collisional orogens: Trans. Royal Soc. Edinburgh: Earth Sciences, 95, 73-85.
• Parker, J.W., Jenkins, J.R., Butler, P.C., Abbott, G.I. (1961) Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. J. Appl. Phys., 32, 1679–1684.
• Pertermann, M. and Hofmeister A.M. (2006) Thermal diffusivity of olivine-group minerals. American Mineralogist, 91, 1747-1760.
• Pertermann M., Whittington A.G., Hofmeister A.M., Spera F.J., and Zayak J. (2008) Thermal diffusivity of low-sanidine single-crystals, glasses and melts at high temperatures. Contrib. Mineralogy and Petrology, 155, 689-702 DOI: 10.1007/s00410-007-0265-x.
• Richet P and Bottinga Y (1995) Rheology and configurational entropy of silicate melts. Reviews in Mineralogy, 32, 67-94.
• Romine, W.L., 2008. Flow and heat transfer properties of Mono Craters rhyolites – effects of temperature, water content and crystallinity. Unpublished MS thesis, University of Missouri, 121 pp.
• Whittington AG, Hofmeister AM, Nabelek PI (2009) Temperature-dependent thermal diffusivity of Earth's crust: Implications for crustal anatexis. Nature, 458, 319-321.
• Yuen, D.A., Vincent, A.P., Bergeron, S.Y., Dubuffet, F., Ten, A.A., Steinbach, V.C., Starin, L., 2000. Crossing of scales and nonlinearities in geophysical processes. In: Boschi, E., Ekstrom, G., Morelli, A. (Eds.), Problems in Geophysics for the New Millenium. Editrice Compositori, Bologna, Italy, pp. 405-465.