 |
Initiation
of Rayleigh–Taylor Instabilities in Intra-Cratonic
Settings |
Weronika Gorczykaa, Bruce
Hobbsa,b, Taras
Geryac
aUniversity of Western Australia (UWA),
Australia
bAustralian Commonwealth
Scientific and Research Organisation (CSIRO), Australia
cSwiss
Federal Institute of Technology Zürich
(ETHZ), Switzerland
weronika.gorczk@uwa.edu.au, bruce.hobbs@csiro.au, taras.gerya@erdw.ethz.ch
This webpage is a summary of Gorczyk,
Weronika, Bruce Hobbs, Taras Gerya, Initiation of
Rayleigh–Taylor instabilities in intra-cratonic
settings, Tectonophysics, 514-517,
146-155, 2012.
Summary
Delamination of the continental mantle lithosphere
can initiate as a result of:
- Mechanical shortening and thickening of the lithosphere
(Houseman
& Molnar 1997; Conrad
2000);
- Density variations between the lithosphere and
asthenosphere, resulting from thermal contraction
(Jull
& Kelemen 2001), or density increases
as a result of metamorphic processes (Elkins-Tanton
2007); and
- Combinations of the above processes coupled with
lateral variations in the plastic strength of the
lithosphere.
Numerical technique
The work described in this webpage
was done using the software I2ELVIS developed by Taras
Gerya (Gerya & Yuen, 2003; Gerya
& Yuen, 2007). I2ELVIS is based on finite
differences schemes and marker-in-cell techniques combined
with a multigrid approach. The code is designed to
model the behaviour of rocks with realistic complex
elasto-visco-plastic rheology, and toaccount
for changes in topography due to erosion-sedimentation
processes and changes in the physical properties of
the rocks due to phase transformations.
The Petrological-Thermochemical
Mode
Mineral phase transformations, such
as dehydration reactions and melting, can affect the
physical properties of rocks during tectonic processes.
The petrological-thermomechanical numerical modeling
approach incorporates, with all in
situ rock properties,
effective density, isobaric heat capacity, thermal
expansion, and adiabatic and latent heating as well
as equilibrium water and melt content. All these rock-,
melt- and fluid-properties are calculated for the
Lagrangian rock markers at every time step, based on
Gibbs free energy minimization (Connolly,
2005) as a function of the local pressure, temperature
and rock composition. In particular, the in
situ rock density
is interpolated for every marker at each time step
from look-up density tables (in P-T space) precomputed
with the PERPLE_X
program for four rock
compositions. To simulate the migration of water released
by dehydration process, we use independently moving
rock and fluid markers (Gorczyk
et al., 2007).
A fluid marker corresponding to a particular water
amount is generated and moves upward until it reaches
a lithology that assimilates water, and can account
for water transport.
How can Rayleigh–Taylor
instabilities be triggered in intra-plate settings?
Studies of mantle lithosphere underneath
old continents (O'Reilly
& Griffin 1996; Begg
et al. 2009; Griffin
et al. 2009) indicate that the SCLMs underneath
these continents are composed of blocks with different
thermal and compositional characteristics. This is
probably a result of strong depletion or extensive
metasomatism during tectonic processes such as subduction
and/or accretion. Figure 1 illustrates the state of
continental crust after 20 Ma of compression at a rate
of 2 cm/a.
Modeling program runs with a homogenous
lithosphere do not develop any strain localization
or mechanical thickening. In contrast, program runs
with a weak zone introduced (which may have been inherited
from the amalgamation of lithospheric blocks, or may
be a post-collisional feature) lead to immediate localization
of strain and thickening of the lithosphere. Rayleigh-Taylor
instabilities may develop later as a consequence.
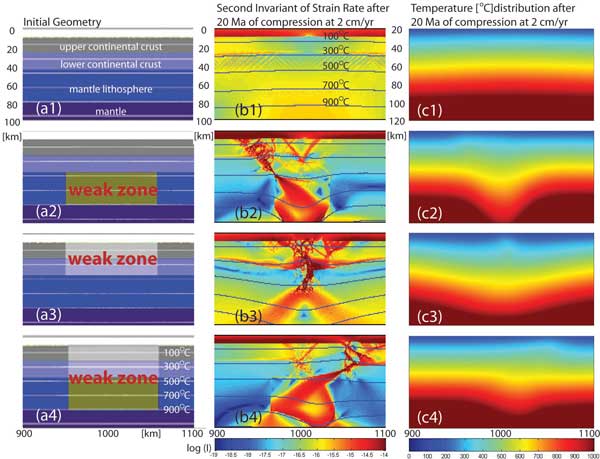
Figure 1. Results of four models
with different initial geometries: (a) initial geometry
and bulk composition, (b) second strain rate invariant
after 20 Ma of compression at rate of 2 cm/a, and
(c) temperature distribution after 20 Ma.
Topographic response
to the classical Rayleigh-Taylor
instability
The ductile detachment of a portion
of the mantle lithosphere (a Rayleigh-Taylor instability)
may result in opposing topographic responses arising
from (1) intra-continental orogeny, and (2) intra-continental
basin formation, as follows.
In the numerical experiments illustrated
in Figures 2 & 3, both of the above phenomena are confirmed.
In the models, topography is influenced by the thickness
of the continental crust above the perturbation. In
cases where the initial perturbation is only imposed
on the mantle lithosphere (Figure 2, column a),
the sinking of the perturbation depresses surface topography
at the axis of symmetry, resulting in basin subsidence
directly above the instability. This effect is illustrated
in Figure 3a where the initial depression of surface
topography is followed by long-lasting relaxation,
leading to extension within the lithosphere after delamination.
Conversely, when an initial thickness
perturbation (a crustal root) is also introduced into
the less-dense continental crust (a continental root),
the topographic response differs drastically (Figures 2b & 3b).
The dynamic evolution of the topography can be described
in three stages:
-
The initial stage is characterized
by uplift (250 m) at the axis of the perturbation
as a result of isostatic equilibration within the
crust;
-
In the second stage, strong
subsidence (100 m) approximately centred on
the axis of symmetry occurs, which leads to the
formation of basins on the sides of the elevated
plateau above the instability. At the same time,
within the plateau area, subtle subsidence takes
place in response to downward displacements arising
from the dripping blob;
-
After detachment of the
downwelling material, isostatic rebound of the
mantle lithosphere takes place. During this final
stage, the base of the continental root heats up,
causing melting of the lower continental crust.
This crustal melting triggers igneous intrusions,
volcanic activity at the surface and the formation
of mountain belts. After the main uplift in the
axial area, further subsidence (~ 2 km) takes place,
expressed as the development of basins on the sides
of the plateau.
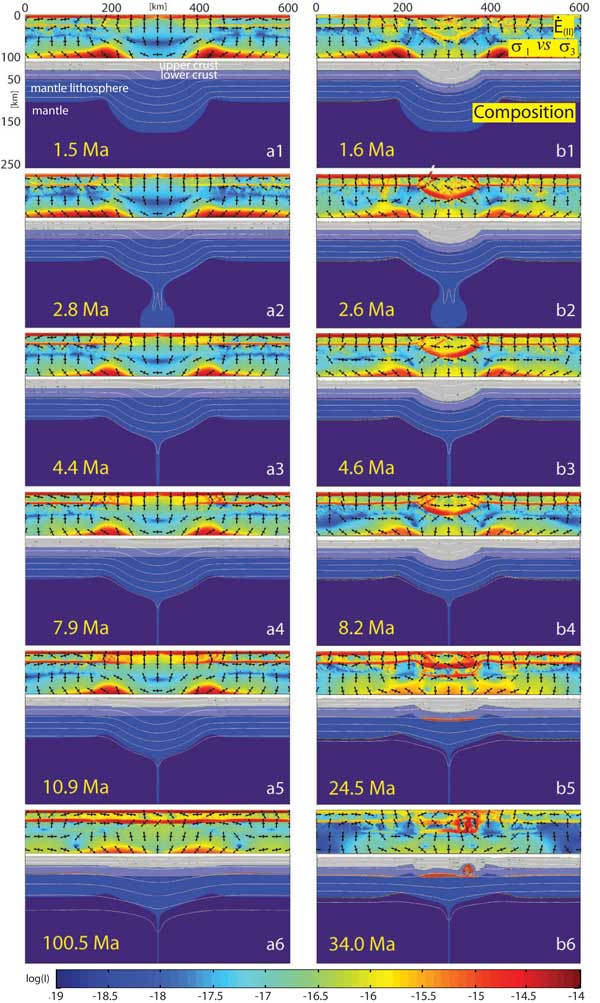
Figure 2. Dynamic
evolution of the lithosphere in two simulations representing
different initial geometries: (a) Initial strength
perturbation imposed only on the mantle lithosphere,
down to 160 km. The initial thickness of the
continent is kept constant across the model. (b)
Initial thickness applied to the mantle lithosphere,
down to 160 km, together with a continental root
reaching down 80 km. Each time-frame is illustrated
by two figures: (i) the upper image represents the
second strain rate invariant) with σ1
v.s σ3 as black crosses, long axis
corresponds to σ3 and short σ1;
(ii) the lower image shows the composition profile
of deformed lithosphere after lapse of indicated time
period.
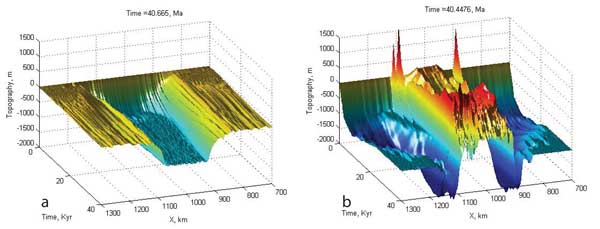
Figure 3. Evolution
of topography above the developing instability corresponding
to the program runs shown in Figure 2:
(a) Program run with initial strength perturbation
imposed only on the mantle lithosphere; and (b) program
run with the initial strength perturbation imposed
on the whole lithosphere but with an additional continental
root. The initial peaks in topography on the sides
of instability occur as a result of initial equilibration
of the topography. Later in the simulation, peaks form
above the downwelling, corresponding to intrusion of
magma into the crust, in addition to mountain-building
processes resulting from the deep lithospheric detachment. Click here or
on figure for enlargement.
Melting and the Rayleigh–Taylor
instability
Melting is triggered during delamination
in the following ways.
- Delamination and sinking of large portions of
lower continental crust allow the influx of asthenosphere
from the low velocity zone. This produces the melts
that form the source of continental flood
basalts (Lustrino,
2005).
- Sinking instabilities may devolatilize (similar
to a descending slab in a subduction zone), and may
themselves also melt, or they may carry volatiles
to depth, depending upon their sinking rate (Elkins-Tanton,
2007).
- Crystalline plasticity could provide a mechanism
for narrow zones of thinning and upwelling. This
could facilitate decompression, and related volcanism
far from plate boundaries (Harig
et al., 2010).
In all three of the above models,
melting of the mantle lithosphere arises from decompression
melting, lowering of the mantle solidus by the introduction
of fluids from hydrated and detached material, or hydrous
heterogeneities that remain long after subduction.
Although the numerical simulations shown in Figure
2b incorporate melting processes, no melting of mantle
lithosphere/asthenosphere occurs as a response to delamitation,
as dry olivine rheology for the mantle is used. Thus,
no hydrous melting is possible. In addition, no decompression
melting of mantle lithosphere and no wholesale detachment
of continental lithosphere occur. On the other hand,
the simulations described here suggest that after the
detachment and sinking of cold, dense materials, elastic
rebound of the remaining lithosphere occurs. In response,
the Moho shallows, pressure decreases, and temperature
increases in the previously thickened part of the crust.
In response, melting of lower crust at the base of
Moho is expected. This may result in additional, extensive
volcanic activity as well as extensive granitic intrusions,
depending on the bulk composition of the lower crust. Dry
olivine rheology for the mantle is used, so no hydrous
melting is possible. In addition, no decompression
melting of mantle lithosphere and no wholesale detachment
of continental lithosphere occur. On the other
hand, the simulations described here suggest that after
the detachment and sinking of cold, dense materials,
elastic rebound of the remaining lithosphere occurs.
In response, the Moho shallows, pressure decreases,
and temperature increases in the previously thickened
part of the crust. In response, melting of lower crust
at the base of Moho is expected. This may result in
additional, extensive volcanic activity as well as
extensive granitic intrusions, depending on the bulk
composition of the lower crust.
References
-
-
Connolly, J.A.D. (2005). Computation of
phase equilibria by linear programming: a tool for
geodynamic modeling and an application to subduction
zone decarbonation. Earth
and Planetary Science Letters 236:
524-541.
-
-
-
-
Gerya, T.V. and D.A. Yuen (2003).
Characteristics-based marker-in-cell method with
conservative finite-differences schemes for modeling
geological flows with strongly variable transport
properties. Physics of the
Earth and Planetary Interiors 140:
295-320.
-
Gerya, T.V. and D.A. Yuen (2007).
Robust characteristics method for modelling multiphase
visco-elasto-plastic thermo-mechanical problems. Physics
of the Earth and Planetary Interiors 163:
83-105.
-
Gorczyk, W., T. V. Gerya, et al. (2007). Melting
and mixing processes in mantle wedges. Geochimica
Et Cosmochimica Acta 71: A346-A346.
-
Gorczyk,
W., B. Hobbs, T. Gerya (2012). Initiation
of Rayleigh–Taylor instabilities in intra-cratonic
settings, Tectonophysics514-517,
146-155.
-
-
-
-
-
-
-
-
-
-
last updated
6th February, 2012 |
