 |
 |
Self-organized
breakup of Gondwana |
|
|
James
W. Sears
University
of Montana, Missoula MT 59812
jwsears@selway.umt.edu |
Abstract
Gondwana
broke apart along a geometrically-regular, truncated-icosahedral
fracture system. This tessellation minimized
total crack length and therefore required the
least work to nucleate and propagate fractures
across the supercontinent. Fracture spacing
was a function of the strength of the Gondwana
lithosphere. Fracture arrangement met conditions
imposed by Euler’s rule for ordering polyhedrons
on a spherical shell. Plates at the vertices
of an icosahedron had five-fold symmetry while
intervening plates had six-fold symmetry. Large
igneous provinces erupted diachronously along
the fractures and triple-junctions. A family
of hot spots are also congruent with the tessellation.
The tensile stress field that initiated the
fractures defined the geometrical dual of the
fracture tessellation (an icosadeltahedron),
for which each vertex corresponds to a face,
and each face to a vertex. The stress field
appears to have been self-organized by the pre-existing
geometry of Gondwana, with tensile hoop-stress
along the passive northern boundary. Regularly-spaced
radial fractures abutted the northern boundary
orthogonally, showing that it acted as a free
surface; these defined the lateral edges of
Australia, India, Arabia, Libya, and northwest
Africa. The polygonal fracture network was symmetrical
about the African geoid bulge when Gondwana
is restored to its Triassic locus. These observations
are consistent with the hypothesis of Anderson
(1982) that Gondwana insulated its underlying
mantle, leading to thermal expansion, uplift
of the African geoid bulge, and fracturing as
Gondwana stretched to accommodate an increased
radius of curvature. The uplift and fracturing
may have culminated during the Triassic marine
lowstand. The fragments then drifted off the
thermal bulge due to plate tectonic demands,
with secondary rifting, large igenous province
eruptions, and lingering hotspot activity. These
observations favor Anderson’s top-down
PLATE paradigm for
the tectonic control of continental breakup
and associated large igneous provinces and hot
spots, and they argue against the deep-mantle-plume
paradigm.
Introduction
While it is generally
agreed that supercontinents break apart and
re-assemble in a grand tectonic cycle, much
controversy surrounds the initiation of the
breakup phase of the cycle (Foulger
et al.,
2005). Following an original idea by J.T.
Wilson (1963), the deep-mantle-plume paradigm
predicts that superadiabatic plumes rising from
the core-mantle boundary drive continental breakup
(Morgan, 1981; Campbell, 2001).
It proposes that the heads of deep mantle plumes
collect at the base of the lithosphere and form
broad domes that split into radiating rifts
(Storey et al., 2001). The plume heads
may then erupt large igneous provinces (LIPs)
from the rifts (Ernst & Buchan,
2001). The rifts may propagate outward and link
together to break up the continent piecemeal
as fragments calve away, perhaps due to secondary
plate tectonic forces. Some active volcanic
hot spots may represent lingering ascents of
thin plume tails (Morgan, 1981). In
this paradigm, plume ascents and breakouts are
episodic and depend upon deep mantle viscosity
and instabilities at the core-mantle boundary
(Steinberger, 2000).
Mantle tomography
and receiver functions do not, however, unequivocally
demonstrate that plumes cross the mantle transition
zone (Foulger
et al.,
2000; Du
et al.,
2006). DeWit et al. (1988), Anderson
(2001;
2002b),
and Hamilton (2002), argue that continental
breakup and associated large igneous outbreaks
and hot spots are controlled, top-down, by lithospheric
processes, rather than by rising plumes. Anderson
(2006) has recently formalized this opposing
view as the PLATE paradigm. Continental breakup
may be initiated by thermal expansion of ordinary
sub-lithospheric mantle that becomes insulated
beneath a stalled or sluggish supercontinent.
For example, Anderson
(1982) showed that the Atlantic-African
geoid anomaly coincides with the late Paleozoic
locus of Pangaea and may represent a residuum
of thermally-expanded sub-Pangaean mantle. The
thermal expansion would lift the supercontinent
and place it under uniform layer-parallel tension
as it adjusted to an increased radius of curvature.
The supercontinent might then rift apart, with
outbreaks of LIPs along rift zones, as fragments
drift off the thermal bulge toward retreating
trenches. Anomalous hot spot activity that continues
at fixed mantle sites within the decaying Atlantic-African
geoid anomaly is consistent with this model
(Anderson,
1982).
Here I argue that
the breakup of Gondwana was self-organized in
accordance with Euler’s theorem for convex
polyhedrons to minimize crack length and therefore
minimize the energy required to nucleate and
propagate fractures. The fracturing appears
to have been controlled by the pre-existing
configuration of the Gondwana margins and the
strength of the Gondwana lithosphere. Plate
tectonic processes later exploited the initial
fractures to widen rifts, trigger hot spots,
release LIPs, and disperse rifted fragments.
This model argues against the deep-mantle-plume
paradigm and supports the top-down tectonic
model of Anderson
(1982).
Gondwanan
fracture tessellation
Figure 1 presents
a standard reconstruction of Gondwana, adapted
from DeWit et al. (1988), Golonka
et al. (1994) and Lawver et al.
(1999). The argument presented in this webpage
follows from recognition that Gondwana’s
initial fracture architecture was closely congruent
with a precise, energy-minimizing configuration,
the truncated icosahedron (Sears
et al.,
2005; Sears, 2001). The truncated
icosahedron comprises a semi-regular polyhedron
made up of 12 pentagonal and 20 hexagonal faces.
The pentagonal faces are centered on the vertices
of an icosahedron. The tessellation is geometrically
intolerant, i.e., a single pentagon fixes the
entire configuration. Projected onto the Earth’s
surface, each tile-edge of a truncated icosahedron
subtends 23.28° of arc, or approximately
2600 km.
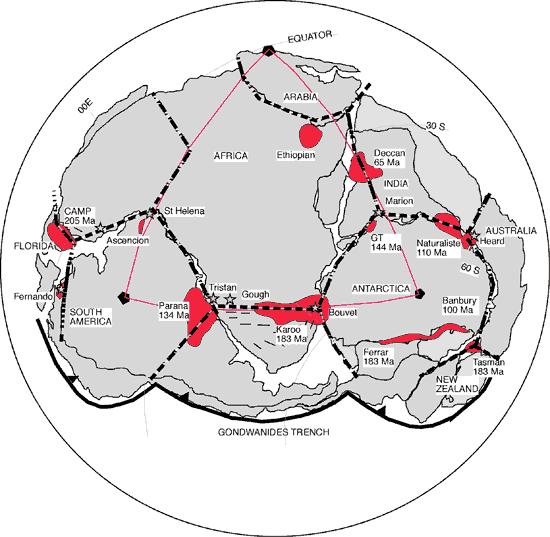
Figure 1. Gondwana
reconstruction at 200 Ma, after Golonka et al.
(1994), Lawver et al. (1999) and DeWit et al.
(1988). Heavy dashed lines are major fractures
that define truncated icosahedral tessellation.
Black pentagons at centers of central South
America, Antarctica, and Arabia occupy vertices
of exact icosahedral triangle (purple) at Earth-scale.
Yellow stars are major hot spot volcanoes in
modern co-ordinates (note lines of latitude
and longitude). Gondwana is restored so that
fracture tessellation best fits hot spot tessellation.
Red areas are LIPs with eruption dates shown.
Note that although dates range over more than
100 million years, most LIPs erupted from fractures
that restore to single tessellation. This implies
that coherent tessellation dates to before oldest
LIP (205 Ma), and that LIPs erupted from fractures
diachronously as later plate tectonics opened
fractures. Click here
or on figure to enlarge.
The Gondwanan
tessellation included all or parts of three
pentagons and six hexagons of the exact scale
and arrangement of a truncated icosahedron at
the Earth’s surface (Figure 1). One measure
of this congruence is that the distance between
the centers of the Antarctic and central South
American pentagons on the reconstruction exactly
equals that between icosahedral vertices (60°
or about 6600 km at Earth-scale). Gondwanan
fractures with a cumulative linear distance
greater than 20,000 km define segments of 16
edges of this truncated icosahedral tessellation.
Their geometric coherence indicates that the
fractures formed in a uniform, Gondwana-wide
stress field prior to dispersal of any daughter
continents. The fractures probably propagated
across Gondwana in Late Permian or early Triassic
time when thermal expansion culminated (Anderson,
1982). The oldest parts of some of the fractures
accumulated Permian or Triassic sediments (Sengor
& Natal’in, 2001). The Late Permian-Early
Triassic marine lowstand (Haq, 1995)
may record the culmination of Gondwana uplift.
Gondwanan
stress tessellation
The Gondwanan
fractures were tensional cracks. Each fracture
thus propagated orthogonally to the local horizontal
principal tensile stress. Construction of the
principal tensile stress direction at the midpoint
of each fracture generates the icosadeltahedron,
the dual polyhedron of the truncated icosahedron
(Figure 2). (Note: Each face of a polyhedron
corresponds to a vertex of its dual. For example,
the cube, with six faces and eight vertices,
represents the dual of the octahedron, with
six vertices and eight faces. The edges of dual
tessellations bisect one another orthogonally.)
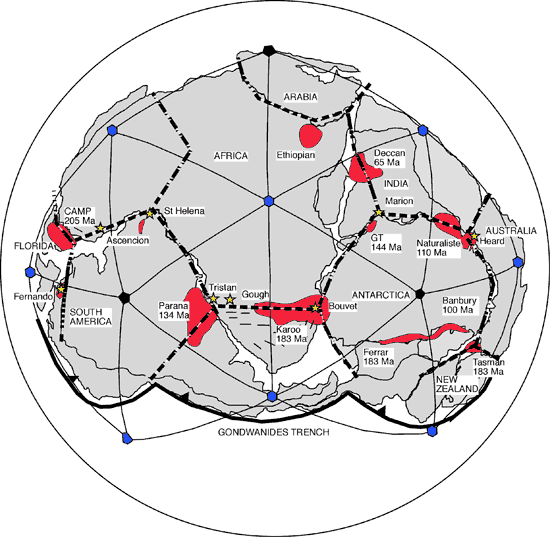
Figure 2. Gondwana
tensile stress tessellation. This icosadeltahedral
tessellation (thin solid lines) is dual of fracture
tessellation (heavy dashed lines) such that
vertices of stress tessellation occupy faces
of fracture tessellation, and vice-versa. Tessellations
cross one another orthogonally. Black vertices
have five nearest neighbors and exactly occupy
vertices of an icosahedron at Earth-scale, as
required by Euler’s rule for convex polytopes
(see text). Blue vertices have six nearest neighbors.
Note that stress tessellation follows northern
margin of Gondwana, implying it was free surface
that guided tensile hoop stress. Thus, Gondwana
split on radial fractures along northern rim.
Note nearly perfect symmetry of stress tessellation
across Gondwana. This provided shortest total
fracture length and thus required least work
to break up Gondwana. Click here
or on figure to enlarge.
The stress tessellation
of Figure 2 obeys Euler’s rule for convex
polytopes. A sphere with n ≥
12 vertices requires 12 vertices with five nearest
neighbors (pentamers) and n-12 vertices
with six nearest neighbors (hexamers). The pentamers
occupy the vertices of an icosahedron. The vertices
in central South America, Antarctica, and Arabia
have five nearest neighbors (not all shown).
As predicted by Euler’s rule, these precisely
occupy the vertices of an icosahedron at the
scale of the Earth. The remaining vertices in
Figure 2 have six nearest neighbors. This precise
geometric relationship indicates that the spherical
Gondwanan shell failed as an integrated whole
in a uniform, non-random fashion.
The edges of Gondwana
appear to have acted as free surfaces that organized
the stress tessellation. Six edges of the stress
tessellation coincided with the northern rim
of Gondwana and parts of the Gondwanides trench
margin.
Tensile hoop-stress
swept around the northern rim of Gondwana from
Central America to New Zealand. Six major radial
Gondwanan fractures abutted this rim because
the fractures formed orthogonally to the tensile
hoop-stress. These fractures separated New Zealand,
Australia, India, Arabia, Libya, northwest Africa,
and Central America. Most of these fractures
were equally spaced, as a function of the strength
of the Gondwanan lithosphere.
Tensile hoop-stress
forms in response to expansion of an enclosed
region. The stress tessellation within the Gondwanan
interior reflected the expansion of the enclosed
Gondwana surface area. It was nearly perfectly
symmetrical across Gondwana, providing the most
balanced stress distribution that was consistent
with the boundary conditions.
The stress field
derived from the fracture tessellation is consistent
with a uniformly and simultaneously expanding
Gondwana, as predicted by the hypothesis of
Anderson
(1982). The plume paradigm predicts, conversely,
that the fractures were caused by random and
unrelated plumes that impinged on the base of
the moving lithosphere.
Scale
of the fracture polygons
The scale of the
fracture tessellation was a function of the
strength of the Gondwanan lithosphere and the
geometry of a spherical shell. The truncated
icosahedral fractures are analogous to the hexagonal
crack patterns seen in columnar-jointed basalt.
For ideally hexagonal basalt columns such as
parts of the Devils
Postpile, Long Valley Caldera, California,
cracks began to form when tension caused by
shrinkage exceeded the strength of the crystallized
and cooling basalt. A planar crack would propagate
to a critical length of about 25 cm, and would
then spontaneously split into two cracks at
an angle of approximately 120° to the original
crack direction. Each new crack would branch
when it reached the critical length and, together
with similar cracks, formed a network of polygonal
columns of surprisingly uniform sizes. Where
a propagating crack encountered the edge of
a flow, it bent into an orthogonal intersection,
because the edge and the propagating crack coincided
with orthogonal principal planes of the local
stress ellipsoid.
Hexagonal fracture
systems develop in an homogenous material undergoing
uniform layer-parallel tension, such as a cooling
and contracting basalt flow, because they provide
the greatest stress relief for the least work
to nucleate and propagate cracks (Jagla
& Rojo, 2002). This is because a regular
hexagonal pattern requires the shortest total
crack length to pave a given area, and provides
the most stable triple-junctions. The energy
used for the work of propagating cracks is stored
as elastic strain within the volume of the contracting
layer. Stronger layers crack into larger hexagons
because fewer tiles are required to pave the
area and these require a shorter total crack
length. More strain energy is required to initiate
the fractures, but because the layer is stronger,
it stores more energy before failing.
Each crack in
an array of hexagonal tension cracks corresponds
to a principal plane of a local stress ellipsoid.
The corresponding local tensile stress is normal
to the crack. Tensile stresses for the entire
hexagonal array of cracks define a triangular
array, with the apices of the triangles at the
centers of the hexagons. The apices form null
points of no strain in the shrinking medium;
strain increases radially outward from them
to the distance at which the material cracks.
Hexagonal close-packing of fractures best relieves
strain between neighboring domains.
The edge lengths
of the polygons increase with strength of the
shell to minimize the total crack length. Once
the polygons become large enough to reflect
the curvature of a spherical shell, Euler’s
rule becomes evident; pentagonal polygons will
occupy the 12 vertices of an icosahedron, and
intervening polygons will be hexagonal. With
increasing shell strength, the 12 pentagonal
faces will increase in size, and the intervening
hexagons will also increase in size because
they share edges with the pentagons. All edge
lengths are equal. The hexagons will decrease
in number in a stepwise fashion to fit the finite
geometry of the sphere. The dodecahedron represents
the strongest configuration for a spherical
shell, with 12 large pentagonal faces and no
intervening hexagons. The truncated icosahedral
Gondwanan fracture tessellation represents the
second strongest configuration, with 12 pentagons
and 20 intervening hexagons for a complete sphere.
Note that Gondwana only occupies a portion of
a sphere.
LIPs
and hot spots
Nine LIPs ranging
in age from Early Jurassic to Early Tertiary
erupted as Gondwana rifted apart and its daughter
continents dispersed. When the continents are
gathered into their Gondwana configuration,
the LIPs are congruent with vertices or edges
of the fracture tessellation. This suggests
that the fracture tessellation prepared the
ascent routes for the eruptive sites, but that
LIP outbreaks depended on later effects such
as decompression melting as plate tectonic movements
widened the fractures and opened conduits for
LIP eruptions.
When Gondwana
is reconstructed, the fracture tessellation
may be superimposed on several major hot spots
associated with Late Jurassic or Early Cretaceous
rifts and LIPs. Heard, Marion, Bouvet, Gough,
Tristan, St. Helena, Ascencion, and Fernando
plot within a few degrees of the tessellation,
mostly near vertices. However, neither older
hot spots associated with opening of the Central
Atlantic (Cape Verde, Canary, Azores), nor younger
hotspots associated with the Deccan or Ethiopian
LIPs are congruent with this position of the
tessellation. The congruent hot spots may record
a time of drift stagnation of Gondwana. Independent
paleomagnetic data indicates that Gondwana moved
in Early Jurassic time, stalled during Late
Jurassic and Early Cretaceous time, and then
rapidly broke apart in Late Cretaceous time
(DeWit et al., 1988; Golonka et
al., 1994).
Eruption of LIPs
may have resulted from decompression melting
upon opening of rifts along the fracture tessellation.
Lingering hot spot activity may have been localized
by alteration of chimneys in the upper mantle
beneath the original sites of the LIP eruptions.
Alternatively, Fairhead & Wilson
(2006) suggest that some hot spot tracks may
be fractures that propagated due to stress instabilities
in the widening plates. Perhaps some hot spots
are due to standing stress waves caused by adaptation
of the symmetry of the fracture tessellation
to the symmetry of sea-floor spreading. These
considerations favor a lithospheric, rather
than deep mantle, control for Gondwana LIPs
and hot spots.
African
geoid anomaly
Anderson
(1982) proposed that the Atlantic-African
geoid anomaly marks the Permian footprint of
Pangaea, the decaying remnant of thermally expanded
mantle that had been insulated beneath the supercontinent.
He proposed further that LIP and hot spot activity
in the region demonstrates its increased thermal
content.
Figure 3 superimposes
a contour map of the African part of the geoid
anomaly on Gondwana in the mantle position it
may have occupied during Triassic time (Golonka
et al., 1994). If the geoid bulge was centered
on Gondwana as shown, then the contours either
paralleled or were orthogonal to the fracture
and stress tessellations.
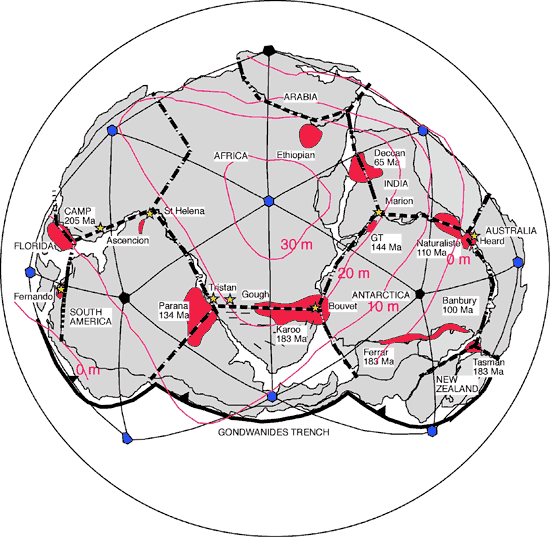
Figure 3. African
geoid anomaly superimposed on Gondwana in its
Triassic position. Note that contours of the
geoid anomaly are generally orthogonal or parallel
to stress tessellation edges, and that anomaly
is centered on Gondwana. This is consistent
with the hypothesis of Anderson
(1982) that the geoid anomaly marks the
paleoposition of Gondwana, and that Gondwana
spread outward from the anomaly as it broke
apart. Click here
or on figure to enlarge.
Anderson
(1982) suggested that Gondwana spread radially
outward from the geoid high, consistent with
the radial components of the stress tessellation.
The outward spreading would also result in hoop
stress parallel to the geoid contours, consistent
with the non-radial components of the stress
tessellation.
The increased
radius of curvature that Gondwanan lithosphere
attained above the geoid anomaly would have
further stretched Gondwana outward, leading
to additional radial and hoop tension. When
the combination of these stresses was large
enough to overcome the strength of the Gondwanan
lithosphere, it cracked into the pattern that
required the shortest total crack length.
The
icosahedron in nature
Comparison of
the Gondwanan tessellation with other natural
examples of icosahedral arrangements provides
insight into the Gondwanan fracture process.
In nature, collections of particles commonly
surface a sphere in icosahedral patterns. These
include blastocysts, colloids, quasi-crystals,
florets, and numerous icosahedral viruses, including
wart, herpes, polio, and HIV (see Anderson,
2002).
Viral
capsids are made up of collections of cells
which are required by Euler’s theorem
for convex polyhedrons to assume icosahedral
configurations like the Gondwana fractures.
Twelve cells have 5-fold coordination (pentamers)
at the vertices of an icosahedron, and the remaining
(n-12) cells have 6-fold coordination
(hexamers). Because the pentamers form shorter,
stronger bonds, bursting viral capsids crack
along hexamers. The cracks zig-zag along polygonal
boundaries much like those on fragmenting supercontinents.
Icosahedral configurations
solve the classic Thomson problem of minimizing
the energy of an array of mutually repulsive
coulombic charges on a sphere (Altschuler
et al., 1997). Twelve charges have five
nearest neighbors and (n-12) have 6
nearest neighbors. The lowest energy configurations
produce truncated icosahedral strain gradients
closely similar to the rift patterns seen on
Gondwana. For the supercontinent, the strain
may have resulted from particles stretching
away from one another to permit the spherical
shell to adapt to an increasing radius of curvature
as the sub-lithospheric mantle thermally expanded.
Conclusions
The self-organized
Gondwana fracture tessellation is consistent
with the hypothesis of Anderson
(1982) that the supercontinent drove its
own breakup by insulating the underlying mantle.
The thermally-expanded mantle lifted Gondwana,
placing it under uniform tension. When the tension
exceeded the strength of the Gondwana lithosphere,
it fractured into a symmetrical polygonal pattern
commiserate with its strength and conforming
to the geometric restrictions of a sphere and
to the boundary conditions of the supercontinent.
Likely, the fractures propagated in zig-zag
fashion across the supercontinent, bending and
branching at critical lengths. The fractures
relieved the tension and separated the supercontinent
into tiles that could move independently under
the influence of plate tectonic processes. Separation
of tiles opened rift valleys and ocean basins
and drove decompression melting of the thermally
expanded mantle, leading to outbreaks of LIPs
and injection of dike swarms. These secondary
effects were diachronous as global plate tectonics
exploited the icosahedral fractures. Stationary
hot spots that mark the eruptive sites of LIPs
may represent long-lasting alterations of LIP
ascent chimneys through the upper mantle, or
tips of fractures fixed by standing stress waves
in growing plates that convert icosahedral symmetry
to plate tectonic symmetry.
References
-
Altschuler,
.L., Williams, T.J., Ratner, E.R., Tipton,
R., Stong, R., Dowla, F., and Wooten, F.,
1997, Possible global minimum lattice configurations
for Thomson’s problem of charges on
a sphere. Physical Review Letters,
78, 2681-2685.
-
-
-
- Anderson,
D. L., 2002b, Plate tectonics as a far-from-equilibrium
self-organized system, in S. Stein & J.
Freymuller, Eds., Plate Boundary Zones,
AGU Monograph, Geodynamics Series 30, p. 411-425.
- Anderson, D.L., 2006, The
PLATE Paradigm, http://www.mantleplumes.org/PLATE.html,
2006.
-
Campbell,
I.H, 2001, Identification of ancient mantle
plumes, in Ernst, R.E., and Buchan, K.L.,
eds., Mantle plumes: Their identification
through time. Geological Society of America
Special Paper 352, 5-21.
-
De
Wit, M., Jeffery, M., Bergh, H., and Nicolaysen,
L., 1988, Geological map of sectors of Gondwana
reconstructed to their disposition ~150 Ma.
America Association of Petroleum Geologists,
Tulsa, OK 74101, scale 1:10,000,000.
-
Ernst,
R.E., and Buchan, K.L., 2001, Large mafic
magmatic events through time and links to
mantle-plume heads, in Ernst, R.E., and Buchan,
K.L., eds., Mantle plumes: Their identification
through time. Geological Society of America
Special Paper 352, 483-566.
- Fairhead, J.D., and Wilson, M.,
2006, Sea-floor spreading
and deformation processes in the South Atlantic
Ocean: Are hot spots needed?, http://www.mantleplumes.org/SAtlantic.html,
2004.
-
-
Foulger,
G.R., Natland, J.H., Presnall, D.C., and Anderson,
D.L., eds., 2005, Plates, plumes, and
paradigms. Geological Society of America
Special Paper 338, 861 pp.
-
Golonka,
J., Ross, M.I., and Scotese, C.R., 1994. Phanerozoic
paleogeographic and paleoclimatic modeling
maps., in A.F. Embry, et al., eds., Pangaea:
Global environments and resources. Canadian
Society of Petroleum Geologists, Calgary,
Canada, 1-47.
-
Hamilton,
W.B., 2002, Plate-tectonic circulation is
driven by cooling from the top and is closed
within the upper mantle. GAC-MAC Annual
Meeting, Saskatoon, Saskatchewan Abstracts,
27, 45.
-
Haq,
.U., 1995, Sea level change. Geotimes,
40, 45-46.
-
Jagla,
E.A., and Rojo, A.G., 2002. Sequential fragmentation:
The origin of columnar quasihexagonal patterns.
Physical Review E 65,
026203, 7 pp.
-
Lawver,
L.A., Gahagan, L.M., Dalziel, I.W.D., 1999.
A tight fit – Early Mesozoic Gondwana,
a plate reconstruction perspective. Mem.
Natl. Ist. Polar Res. Spec Issue 53,
214-229.
- Lawver, L.A., Dalziel, I.W.D.,
and Gahagan, L.M., 1999. Antarctica
– Keystone of Gondwana, http://www.ig.utexas.edu/research/projects/plates.
-
Morgan,
W.J., 1981, Hot spot tracks and the opening
of the Atlantic and Indian Oceans, in C. Emiliani,
ed., The Sea. Wiley, NY, 7, 443-487.
-
Sears,
J.W., 2001, Icosahedral fracture tessellation
of early Mesoproterozoic Laurentia. Geology,
29, 327- 330.
-
-
Sengor,
A.M.C., and Natal’in, B.A., 2001, Rifts
of the world, in Ernst, R.E., and Buchan,
K.L., eds., Mantle plumes: Their identification
through time. Geological Society of America,
Special Paper 352, 389-482.
-
Steinberger,
B., 2000, Plumes in a convecting mantle: Models
and observations for individual hotspots.
Journal of Geophysical Research,
105, 11,127-11,152.
-
Storey,
B.C., Leat, P.T, and Ferris, J.K., 2001, The
location of mantle-plume centers during the
initial stages of Gondwana breakup, in Ernst,
R.E., and Buchan, K.L., eds., Mantle plumes:
Their identification through time. Geological
Society of America, Special Paper 352, 71-80.
-
Wilson,
J.T., 1963, A possible origin of the Hawaiian
Islands. Canadian Journal Physics,
41, 863-868.
|
last
updated 26th April, 2006 |
|
|
|
