The effect of composition, temperature, and pressure on the elasticity of olivine and garnet: Implications for interpreting seismic velocity variations in the mantle

Akira Yoneda¹, Ganglin Chen², Hartmut A. Spetzler³, and Ivan C. Getting⁴

¹Inst. for Study of the Earth's Interior, Okayama Univ., Misasa, Tottori 682-0193, Japan; yoneda@misasa.okayama-u.ac.jp

²ExxonMobil Upstream Research Company, Houston, Texas, U.S.A.; ganglin.chen@exxonmobil.com

³Emeritus Professor/Fellow, Geological Sciences/CIRES, Univ. Colorado at Boulder, Boulder, Colorado, U.S.A.; hartmut.spetzler@Colorado.EDU

⁴Senior Research Associate Emeritus, CIRES, Univ. Colorado at Boulder, Boulder, Colorado, U.S.A.; Getting@Colorado.EDU

Abstract

Composition, temperature, and pressure are all factors that can affect seismic velocity in the mantle. Laboratory elasticity data show that a decrease of 1% in the Mg/(Mg+Fe) ratio in olivine reduces the velocity by an amount equivalent to that caused by a temperature increase of 70 K. The compositional effect of pyrope-almandine garnet on seismic velocity is similar to that of olivine, though slightly smaller. If the upper mantle is composed mainly of olivine, and if the relationships obtained from laboratory measurements between elasticity, temperature, and composition hold at the P-T conditions appropriate to the mantle, then variations of only 1-2% in the Mg/(Mg+Fe) content of olivine can account for all the observed variation in dlnVp in the mantle. Other factors such as temperature may also vary, but such effects may not be required to explain observed velocity variations.

Introduction

Seismic velocity profiles of the mantle enable Earth scientists to probe mantle structure. Potential mantle plume locations are of particular interest. Technological advances in seismic hardware and software have led to a proliferation of models and interpretations related to mantle heterogeneity, anisotropy, and anelasticity. However, as Don L. Anderson pointed out elegantly in his article “Is there convincing tomographic evidence for whole mantle convection”, it is not safe to simply assume that seismic tomography is a mantle thermometer. In fact, composition, temperature, and pressure are just some of the factors that can contribute to seismic velocity variations. To facilitate the interpretation of global seismological data, precise elasticity data for mantle minerals are needed. In this short article, we review some measurements of the elasticity of mantle minerals with relevant background material that we hope may stimulate further interest and discussion of this topic.

Several factors affect acoustic and elasticity data acquired in the laboratory, including composition, temperature, pressure, wave frequency, and mineral texture. These are also the parameters that affect seismic velocities in the mantle. Experimentalists can design controlled experiments to separate the effect of one parameter from the others. The laboratory techniques to measure elasticity of minerals include Brillouin Light Scattering (BLS; Weidner et al., 1982), Impulsive Stimulated Light Scattering (ISLS; e.g., Crowhurst, 2006), GHz Ultrasonic Interferometry (GUI; Spetzler et al., 1993), Multi-anvil Ultrasonics (Liebermann et al., 1998), Inelastic X-ray Scattering (IXS; e.g., Fukui et al., 2008), and high-frequency extension of Resonant Ultrasound Spectroscopy (RUS; Yoneda et al., 2007). BLS was introduced by Weidner et al. (1982) to measure single crystal Stishovite and has been used for elasticity measurements at pressures above 100 GPa in diamond anvil cells (DAC; e.g., Murakami et al., 2007a;b). A recent study by Mao et al. (2008) shows that 1 wt% of H₂O in wadsleite decreases bulk modulus and rigidity by ~10 %.

A fundamental disadvantage of BLS is that it is not suitable for measurements on opaque minerals such as some mantle minerals that contain substantial amounts of divalent iron (Fe⁺²). To overcome this problem, ISLS was introduced (e.g., Crowhurst, 2006). ISLS can be used even in the case of metal samples. Another experimental challenge for BLS and ISLS is to conduct high pressure measurements in DAC in which the P-mode (compressional wave) scattered peaks from the sample tend to overlap with the S-mode (shear wave) from the diamond anvil.

To overcome these difficulties, GUI was developed. The innovative GUI instrumentation is based on the rapid progress in digital oscilloscope technology in the early 1990s (Spetzler et al., 1993). The unprecedented high-precision acoustic velocity data (to 1 part in 10^-6) on minerals of sub-millimeter sizes obtained by GUI opened up new opportunities for mantle mineral elasticity studies. Measurements were made of selected elastic moduli of some mantle minerals to illustrate the effect of temperature, composition, and simultaneous pressure and temperature (Chen et al., 1996a, 1996b; Chen et al., 1997).

Results and Discussion

Figure 1 (Figure 5 from Chen et al., 1996a, reproduced) summarizes the GUI measurement results of the compositional dependence of the temperature derivatives for two selected elastic moduli in the forsterite-fayalite olivine solid solution series and the pyrope-almandine garnet solid solution series. The results show that the temperature derivatives of the elastic moduli of olivine and garnet decrease systematically with decrease in the Mg/(Mg+Fe) ratio. Furthermore, the results indicate the trade-off effect of composition and temperature on the elasticity or acoustic velocities of these mantle minerals. For example, a decrease of 1% in Mg/(Mg+Fe) ratio in olivine reduces the velocity by an amount equivalent to that caused by a temperature increase of 70 K.

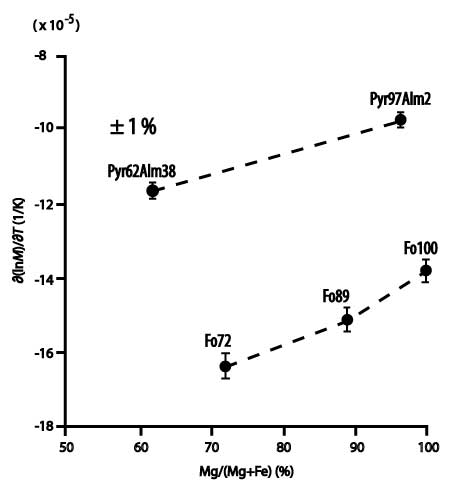
Figure 1 : Summary of the temperature derivatives for olivine ∂lnC₂₂/∂T and garnet ∂ln[C₄₄+(C₁₁-C₁₂)/2]/∂T. Note the 1% error bar in this figure (Figure is reproduction of Figure 5 in Chen et al., 1996a).

Seismic tomography shows that the lateral variation of seismic velocity in the upper mantle is about 0.5% for dlnVp within a single tectonic region (e.g., Pulliam et al., 1993). Such lateral velocity variation has been attributed to lateral temperature variations in the upper mantle. If the upper mantle is composed mainly of olivine, and if the relationships obtained from our laboratory measurements between elasticity, temperature, and composition hold at the P-T conditions appropriate to the mantle, then the observed variation in dlnVp can be accounted for by only 1-2% variation in the Mg/(Mg+Fe) content of olivine. The composition of San Carlos olivine has been found to range from 89% to 92.7% (Isaak, 1992). Such a variation may originate from compositional inhomogeneities in the sources of these olivines in the upper mantle.

It is possible that both temperature and composition vary in the upper mantle and contribute to observed lateral seismic velocity variations. If we had information on lateral density variations from regions that exhibit lateral seismic velocity variation, we would be able to constrain whether the observed seismic velocity variations originated in temperature variations or in compositional variations. If the Fe content causes lateral seismic velocity variation in the upper mantle, then low-velocity regions will be denser than high-velocity regions. The relationship is the opposite if temperature variations cause low velocities–then hot, low-velocity regions will be less dense than cold, high-velocity regions. Consequently the resultant mantle convection scheme, whether bodies sink, float, or rise, will be quite different. Trampert et al. (2004) showed that there are regions in the mantle where low velocities characterize high-density regions, not high-temperature regions (i.e., the ‘superplumes’).

In a continuation of this laboratory measurement work, Chen et al. (1997) were able to complete the measurements of the elasticity systematics for the pyrope-almandine solid solution series using GUI as a result of H. Spetzler’s persistent and successful effort to develop the technique to achieve shear wave measurements at GHz frequencies. The effect of the Mg/(Mg+Fe) ratio on the elasticity of pyrope-almandine series samples was shown to be comparable to olivine in magnitude, albeit smaller. A 10% decrease in Mg/(Mg+Fe) reduces the acoustic velocity in pyrope-almandine by about 1% vs. a 3% reduction in Vp[010] for olivine. The high precision of the GUI data also allows measurement of the mixed pressure and temperature derivatives of olivine (Chen et al., 1996a). The results indicate that the cross pressure and temperature dependence of the acoustic velocities of olivine may need to be considered when interpreting seismic velocity data in terms of mantle structure. The temperature dependences of the elastic constants for three important mantle minerals: β-spinel, γ-spinel, and perovskite (Aizawa, 2004; Mayama, 2004, 2005) became available as a result of the effort led by Akira Yoneda.

The magnitude of the mixed pressure and temperature derivatives of sound velocities and elastic moduli of mantle minerals can also affect interpretations in terms of of mantle structure, e.g., Karki et al. (1999). Chen et al. (1996b) used the high precision offered by GUI to measure selected mixed pressure and temperature derivatives for olivine (Figure 2). Gwanmesia et al. (2006) reported the results on synthetic pyrope garnets by combining gas- and solid-pressure medium data. The magnitude of the mixed derivatives for these mantle minerals is of the order of 10^-3 to 10^-4. As a result, the pressure dependence of elasticity determined at ambient or close-to-ambient temperature must be corrected for the temperature effect in order to apply to mantle conditions. The same is true for the temperature dependence of elasticity determined at ambient or close-to-ambient pressure. Because the mixed derivatives are so small, extremely high precision elasticity data are needed.

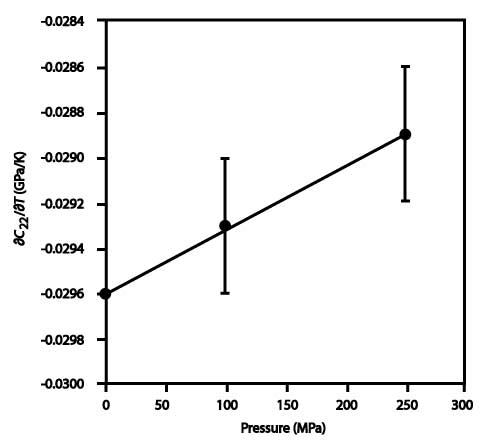
Figure 2 : Temperature derivative of C₂₂ for San Carlos olivine vs. pressure with a lapped contact. The straight line is a linear fit. The uncertainties in the temperature derivatives are a maximum of about 2% and result from the propagation the uncertainties in the travel-time and the temperature data (Figure is reproduction of Figure 3 in Chen et al., 1996b ).

The continuing demand for high precision elasticity data suitable for interpreting seismic velocity profiles of the mantle stimulated further GUI instrumentation to be developed for use at high pressures (Jacobsen et al., 2002; 2004; Kantor, 2004). Other innovative methods were also developed such as RUS (Maynard, 1996; Yoneda et al., 2007), IXS (e.g., Antonangeli et. al., 2005; Fiquet et. al., 2009), and ultrasonics in multi-anvil cells for single crystals (Chen et al., 1998). Measurement capability has now been extended to lower-mantle pressures (Murakami et al., 2007a;b, 2009a, 2009b). Single crystal wadsleyite has successfully been grown (Shatskiy et al., 2009). These developments have provided, and will continue to provide, important constraints on seismic data interpretations aimed at understanding the mantle. Table 1 compares some of the measurement techniques used for single-crystal mantle minerals.

Table 1. Comparison of elasticity measurement techniques that are useful for single-crystal mantle minerals.

* Transparency is not needed for Stonely wave excitation. However elastic properties of the liquid medium is required for the analysis.
** (HRUS–High-frequency Resonant Ultrasound Scattering). In the case of a spherical shape, determining the crystallographic orientation can be omitted.

We conclude by emphasizing that there are two major subjects that must be bourn in mind when laboratory elasticity data on single crystals of mantle minerals are applied to interpretations of global seismic velocity data–the textural effect (anisotropy), and the frequency effect (velocity dispersion). We refer to the excellent papers on these subjects by Getting et al. (1997), Jackson et al. (2002, 2004), Mavko et al. (2009), Karato (1993), and Karato & Karki (2001).

References

• Aizawa, Y., Yoneda, A., Katsura, T., Ito, E., Saito, T., Suzuki, I., 2004. Temperature derivatives of elastic moduli of MgSiO₃s perovskite, Geophys. Res. Lett., 31, L01602, doi:10.1029/2003GL018762.
• Antonangeli, D., Krisch, M., Fiquet, G., Badro, J., Farber, D. L., Bossak, A., Merkel, S., 2005. Aggregate and single-crystalline elasticity of hcp cobalt at high pressure, Phys. Rev. B, 72, 13,4303.
• Chen G., Spetzler, H. A, Getting, I. C.,. Yoneda A., 1996a. Selected elastic moduli and their temperature derivatives for olivine and garnet with different Mg/(Mg+Fe) contents: Results from GHz ultrasonic interferometry, Geophys. Res. Lett., 23, 5-8.
• Chen G., Yoneda A., Getting, I. C., Spetzler, H. A., 1996b. Cross pressure and temperature derivatives of selected elastic moduli for olivine from gigahertz ultrasonic interferometry, J. Geophys. Res., 101, 25,161-25,171.
• Chen, G., Miletich, R., Mueller, K., and Spetzler, H.A., 1997. Shear and compressional mode measurements with GHz ultrasonic interferometry and velocity-composition systematics for the pyrope-almandine solid solution series, Phys. Earth Planetary Int., 99, 273-287.
• Chen, G., Liebermann, R.C., and Weidner, D.J., 1998. Elasticity of single-crystal MgO to 8 Gigapascals and 1600 Kelvin, Science, 280, 1913-1916.
• Crowhurst, J. C., Antonangeli, D., Brown, J. M., Goncharov, A. F., Faber, D. L., Aracne, C. M., 2006. Determination of the high pressure elasticity of cobalt from measured interfacial acoustic wave velocities, Appl. Phys. Lett., 89, id: 111920 (3 pages).
• Fiquet, G., Badro, J., Gregoryanz, E., Fei, Y., Occelli, F., 2009. Sound velocity in iron carbide (Fe3C) at high pressure: Implications for the carbon content of the Earth’s inner core, Phys. Earth Planet. Inter., 172, 125-129.
• Fukui, H., Katsura, T., Kuribayashi, T., Matsuzaki, T., Yoneda, A., Ito, E., Kudoh, Y., Tsutsui, S., Baron, A. Q. R., 2008. Precise determination of elastic constants by high-resolution inelastic X-ray scattering, J. Synchrotron Radiation, 15, 618-623.
• Getting, I. C., Dutton, S. J., Burnley, P. C., Karato, S., Spetzler, H. A., 1997. Shear attenuation and dispersion in MgO, Phys. Earth Planet. Inter., 99, 249-257.
• Gwanmesia, G., Jackson, I., and Liebermann, R. C., 2006. In search of the mixed derivative d2M/dPdT (M = G, K): joint analysis of ultrasonic data for polycrystalline pyrope from gas- and solid-medium apparatus, Phys. Chem. Minerals, 34, 85-93.
• Jackson, I., Faul, U. T., FritzGerald, D. F., Tan, B. H., 2004. Shear wave attenuation and dispersion in melt-bearing olivine polycrystals: 1. Specimen fabrication and mechanical testing, J. Geophys. Res., 109, doi: 10.1029/2003JB002406.
• Jackson, I., FritzGerald, D. F., Faul, U. T., Tan, B. H., 2002. Grain-size-sensitive seismic wave attenuation in polycrystalline olivine, J. Geophys. Res., 107, doi: 10.1029/2001JB001225.
• Jacobsen, S. D., Reichmann, H., Spetzler, H. A., Mackwell, S. J., Smyth, J. R., Angel, R. J, McCammon, C. A., 2002. Structure and elasticity of single-crystal (Mg,Fe)O and a new method of generating shear waves for gigahertz ultrasonic interferometry, J. Geophys. Res., 107, doi: 10.1029/2001JB000490.
• Jacobsen, S. D., Smyth, J. R., Spetzler, H. A., Holl C. M., Frost, D. J., 2002. Sound velocities and elastic constants of iron-bearing hydrous ringwoodite, Phys. Earth Planet. Inter., 143-144, 47-56.
• Kantor, A. P, Jacobsen, S. D, Kantor. I. Y, Dubrovinsky, L. S., McCammon, C. A., Reichmann, H. J., Goncharenko, I. N., 2004. Pressure-induced magnetization in FeO: Evidence from elasticity and Mossbauer spectroscopy, Phys. Rev. Lett., 93, Issue: 21 Article Number: 215502.
• Karato, S., 1993. Importance of anelasticity in the interpretation of seismic tomography, Geophys. Res. Lett., 20, 1623-1626.
• Karato, S., Karki, B. B., 2001. Origin of lateral variation of seismic wave velocities and density in the deep mantle, J. Geophys. Res., 106, 21771-21783.
• Karki, B. B., Wentzkovitch, R. M., de Gironcoli, S., Baroni, S., 1999. First principles determination of elastic anisotropy and wave velocities of MgO at lower mantle conditions, Science, 286, 1705-1707.
• Liebermann, R.C., G. Chen, B. Li, G.D. Gwanmesia, J. Chen, M.T. Vaughan, and D.J. Weidner, Sound Velocity Measurements in Oxides and Silicates at Simultaneous High Pressures and Temperatures using Ultrasonic Techniques in Multi-Anvil Apparatus in Conjunction with Synchrotron X-radiation Determination of Equation of State, in The Review of High Pressure Science & Technology, 7, 75-78, 1998.
• Mao Z., Jacobsen, S. D., Jiang, F., Smyth, J. R., Holl, C. M., Frost, D. J., Duffy, T. S., 2008. Single crystal elasticity of wadsleyite, β-Mg₂SiO₄, containing 0.37-1.66 wt. % H₂O, Earth Planet. Sci. Lett., 266, 78-89.
• Mavko, G., Mukerji, T., Dvorkin, J., 2009. The Rock Physics Handbook, Second Edition, Cambridge University Press (Cambridge, England).
• Mayama, N., Suzuki, I., Saito, T., Ohono, I., Katsura, T., Yoneda, A., 2004. Temperature dependence of elastic moduli of β-(Mg, Fe)₂SiO₄, Geophys. Res. Lett. 31, L04612, 10.1029/2003GL019247.
• Mayama, N., Suzuki, I., Saito, T., Ohono, I., Katsura, T., Yoneda, A., 2005.Temperature dependence of the elastic moduli of ringwoodite, Phys. Earth Planet. Int., 148, 353-359.
• Maynard, J., 1996. Resonant ultrasound spectroscopy, Phys. Today, 49, 26-31.
• Murakami, M., Ohishi Y., Hirao, N., Hirose, K., 2009a. Elasticity of MgO to 130 GPa: Implications for lower mantle mineralogy, Earth Planet. Sci. Lett., 277, 123-129.
• Murakami, M., Sinogeikin, S. V., Bass, J. D., Sata N., Ohishi Y., Hirose K., 2007a. Sound velocity of MgSiO3 post-perovskite: A constraint on the D” discontinuity, Earth Planet. Sci. Lett., 259, 18-23.
• Murakami, M., Sinogeikin, S. V., Hellwing, H., Bass, J. D., Li, J., 2007b. Sound velocity of MgSiO₃ perovskite to Mbar pressure, Earth Planet. Sci. Lett., 256, 47-54.
• Murakami, M., Sinogeikin, S. V., Litasov, K., Ohtani, E., Bass, J. D., 2009b. Single-crystal elasticity of iron-bearing majorite to 26 GPa: Implications for seismic velocity structure of the mantle transition zone, Earth Planet. Sci. Lett., in press.
• Pulliam, R. J., Vasco, D. W., Johnson, L. R., 1993. Tomographic inversion for mantle P wave velocity structure based on the minimization of l2 and l1 norms of intenational seismological center travel time residuals, J. Geophys. Res., 98(B1), 699-734.
• Shatskiy, A., Litasov, K. D., Matsuzaki, T., Shinoda, K., Yamazaki, D., Yoneda, A., Ito, E., Katsura, T., Single Crystal Growth of Wadsleyite, Am. Mineragist, in press.
• Spetzler, H.A., G. Chen, S. Whitehead, and I.C. Getting, 1993. A New Ultrasonic Interferometer for the Determination of Equation of State Parameters of Sub-Millimeter Single Crystals. Phys. Earth Planet. Inter., 141, 341-377.
• Trampert, J., Deschamps, F. Resovsky, J. & Yuen, D. 2004, Probabalistic tomography maps chemical heterogeneities throughout the lower mantle, Science, 306, 853–856.
• Weidner, D. J., Bass, J. D., Ringwood, A. E., Sinclair, W., 1982. The single-crystal elastic moduli of stishovite, J. Geophys. Res., 87, 4740-4746.
• Yoneda, A., Ichihara, M., Shear viscoelasticity of ultrasonic couplers by broadband reflectivity measurements, J. Appl. Phys., 97, 054901, 2005.
• Yoneda, A., Aizawa, Y., Rahman, M., Sakai, S., 2007. High Frequency Resonant Ultrasound Spectroscopy to 50 MHz: Experimental Developments and Analytical Refinement, Jpn. J. Appl. Phys., 46, 7898-7903.

Comments & discussion

3rd September, 2009
Andy Moore (African Queen Mines Ltd., Botswana & Dept. Geology, Rhodes University, South Africa)

This webpage underlines all of my prejudices about geophysical modeling. If you look at the results of the seismic array across the Kaapvaal-Zimbabwe cratons, with one of the best (highest density) array of receiver stations, most of the P and S wave velocity anomalies show a variation of ± 0.5%, but the papers presenting these data do not specify the 2-sigma errors on these estimates, which are based on a variety of poorly constrained variables. No geochemist would be allowed to get away with such liberties in data presentation–or shouldn’t.

last updated 3rd September, 2009