|
Clinton P. Conrad1,
Todd A. Bianco2 & Eugene I. Smith3
1Dept.
Geology & Geophysics, Univ. Hawaii at Manoa,
Honolulu HI 96822, clintc@hawaii.edu
2Dept.
Geology & Geophysics, Univ. Hawaii at Manoa,
Honolulu HI 96822, tbianco@hawaii.edu
3Dept.
Geoscience, Univ. Nevada at Las Vegas, Las Vegas
NV 89154, gene.smith@unlv.edu
This webpage is
a summary of: Conrad,
C.P., B. Wu, E.I. Smith, T.A. Bianco, and A. Tibbetts,
Shear-driven upwelling induced by lateral viscosity
variations and asthenospheric shear: A mechanism
for intraplate volcanism, Physics of the Earth
and Planetary Interiors, 178,
162-175, 2010.
Introduction
Most of the volcanism around the
globe occurs at subduction zones and mid-ocean
ridges, and is well-explained by the theory of
plate tectonics. Volcanism that occurs away from
plate boundaries, however, is less readily explained,
but has often been attributed to hot plumes that
rise from deep within the mantle [Morgan,
1971]. However, several intraplate volcanic features
are not associated with classic hotspot tracks
(e.g., the Cretaceous seamounts that pervade
the western Pacific basin [Hillier & Watts,
2007] or the mid-Miocene to contemporary basaltic
volcanic fields of the southwestern US [Smith
et al., 2002]). Without a deep-mantle source
of excess heat, most alternative explanations for
intraplate volcanism invoke some source of regional
asthenospheric upwelling that induces decompression
melting of near-solidus fertile mantle [Raddick
et al., 2002; Hernlund et al., 2008].
Several upwelling mechanisms have been proposed
such as small-scale thermal convection in the asthenosphere
[e.g., Haxby & Weissel, 1986; van
Hunen & Zhong, 2006; Ballmer et al.,
2007; Ed: see also Small-scale
Convection], return flow from occasional “drips” of
dense lithosphere sinking into the upper mantle
[e.g., Le Pourhiet et al., 2006],
and “edge-driven” convection near sharp
gradients in lithospheric thickness [e.g., King & Anderson,
1998; King & Ritsema, 2000; Ed: see
also Edge Convection].
These mechanisms for driving asthenospheric upwelling
utilize the density inversion between the lithosphere
and asthenosphere as an energy source.
Conrad et al. [2010] demonstrated an alternative mechanism for generating
intraplate upwelling. This mechanism, named “Shear-Driven
Upwelling” (SDU), is based on asthenospheric
shear, which accommodates the few cm/yr of relative
motions between surface plates and the convecting
mantle. SDU is a variation of “shear-driven
cavity flow”, a classic engineering problem
in which shear flow in a channel induces circulatory
flow within an adjacent fluid-filled cavity [e.g., Shen & Floryan,
1985; Pakdel et al., 1997; Shankar & Deshpande,
2000]. Applied to the asthenosphere, the driver
for SDU is the relative motion between the plates
and mantle; upwelling flow is excited in this case
by lateral viscosity heterogeneity (e.g.,
Figure 1), rather than by density heterogeneity.
Below, we summarize the analysis of Conrad
et al. [2010] of how SDU can generate mantle
upwelling and intraplate volcanism.

Figure 1: Diagram showing two
mechanisms by which asthenospheric shear can
act on lateral viscosity heterogeneity to induce
Shear-Driven Upwelling (SDU). Asthenospheric
shear is generated by relative motion between
the mantle and the lithosphere, and is drawn
here in a lithospheric reference frame. Shearing
asthenosphere can induce (a) “shear-driven
cavity flow” within a variation in lithospheric
thickness or (b) circulatory flow within a “pocket” of
low-viscosity asthenosphere. Both flows induce
upwelling; if the asthenospheric mantle is fertile
and near its solidus, melting and surface volcanism
can result.
SDU within a Lithospheric
Cavity
To examine the response of asthenospheric
shear flow to a variation in the basal topography
of the lithosphere, we use the two-dimensional
finite element code ConMan [King et
al., 1990] and generate asthenospheric shear
flow by imposing rigid velocity boundary conditions
above and a dimensionless velocity V below
a viscous asthenospheric channel (Figure 2a). Above
the asthenosphere lies a stationary high viscosity
lithospheric layer in which a cavity is embedded.
For narrow cavities, circulatory flow fills the
entire cavity (Figure 3a) and SDU occurs along
the downstream wall of the cavity. As the aspect
ratio grows (Figure 3b), the circulatory flow is
confined to the two inner corners of the cavity
while the rest of the cavity becomes filled with
a broad widening of the background asthenospheric
shear flow. As the cavity widens further (Figure
3c), the penetration of asthenospheric shear into
the cavity dominates the cavity flow field and
generates SDU on the upstream side of the cavity.
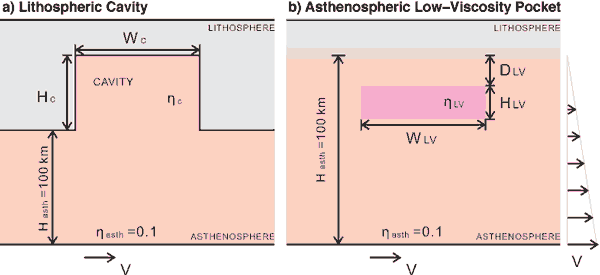
Figure 2: Drawings of asthenospheric
shear flow (driven by an imposed basal velocity
of V) beneath a stationary lithosphere that features
(a) a “cavity” of variable height
HC and width WC and viscosity  ,
and (b) an embedded “pocket” of low-viscosity
fluid of variable height HLV, width WLV, depth
DLV, and viscosity hLV, as shown. ,
and (b) an embedded “pocket” of low-viscosity
fluid of variable height HLV, width WLV, depth
DLV, and viscosity hLV, as shown.
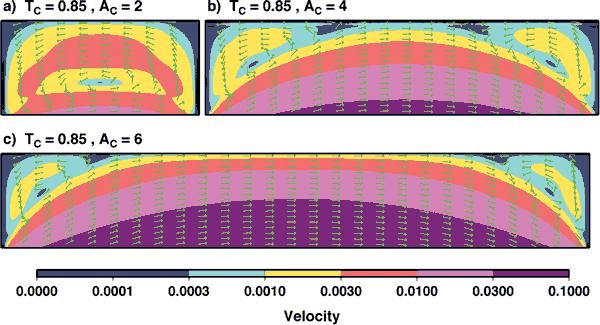
Figure 3: Calculations of the
flow field within the cavity shown in Figure
2a, for three different cavity aspect ratios
(AC,=WC/HC) and a single cavity depth given by
the athenospheric thickness ratio TC= Hasth /(Hasth+HC)
=0.85. Arrows indicate direction of flow, and
colors indicate velocity magnitude as fraction
of V, the imposed velocity at the base of the
asthenosphere. Three different patterns of flow
are shown. (a) For small aspect ratios (AC=2),
the cavity is narrow enough that the asthenospheric
shear flow cannot penetrate into the cavity and
a closed circulation develops. (b) In a wider
cavity (AC=4), asthenospheric shear penetrates
into the cavity and individual circulatory cells
develop in the corners of the cavity. (c) For
larger aspect ratios (AC=6), asthenospheric shear
dominates in the center of the cavity, but weak
circulation persists in the cavity corners.
On Earth, lithospheric thickness
variations are found at mid-ocean ridges, continental
rifts, and cratonic edges. Near a mid-ocean ridge,
the lithospheric basal depth can vary by up ~30
km over a ~400 km wide region. Such a wide and
shallow cavity is not conducive to SDU. Continental
rifting may generate narrower and deeper cavities.
For example, tomography of the Rio Grande rift
[West et al., 2004] shows a ~200 km wide
by ~100 km deep low-velocity anomaly [van Wijk
et al., 2008]. Asthenospheric shear flow of
5 cm/yr beneath this cavity would induce a closed
circulation (e.g., Figure 3a) and SDU
of ~0.2 cm/yr (4% of the shear amplitude), along
the rift cavity’s downstream wall. Finally,
the downstream-facing edge of a craton extending
from 100 to 200 km depth should generate SDU with
magnitudes ~10% of the driving shear amplitude,
or about 0.5 cm/yr for 5 cm/yr of driving shear.
These rates of upwelling can generate melt at rates
up to 0.3 and 0.8 km/Myr, respectively, assuming
near-solidus asthenosphere and typical melt parameters
[Phipps Morgan, 2001; Raddick et al., 2002].
SDU within
an Asthenospheric Low-Viscosity “Pocket”
A geophysically-interesting variation
of the shear-driven cavity flow, which has not
been explored in the engineering literature, involves
relaxing the rigidity of the cavity-containing
layer. In this case, the “cavity” becomes
a region of relatively low-viscosity embedded within
the shearing layer (Figure 1b). To study the response
of asthenospheric viscosity heterogeneity to imposed
shear flow, we embed a rectangular “pocket” of
low-viscosity fluid within a shearing asthenospheric
layer (Figure 2b). We find that circulatory flow
develops for a certain range of pocket aspect ratios
and thicknesses because the deformation preferentially
localizes within the low-viscosity pocket, rather
than within the surrounding high-viscosity asthenosphere.
If the pocket’s vertical extent spans a more
than ~70% of the asthenosphere thickness (Figure
4a), then the background shear flow overwhelms
circulatory flow. Alternatively, circulatory flow
cannot develop within a small pocket (Figure 4c)
because it is energetically inefficient. Only for
pockets with aspect ratios greater than ~6 and
thicknesses between 20% and 60% of the asthenospheric
thickness is circulatory flow excited by the driving
shear flow (Figure 4b). For a pocket that is 100
times less viscous than the asthenosphere, the
maximum upwelling velocity occurs on the downstream
edge of the pocket at rates up to ~20% of the maximum
shear velocity contrast. Considering 5 cm/yr of
driving shear flow, then the rate of upwelling
flow could be up to 1 cm/yr.
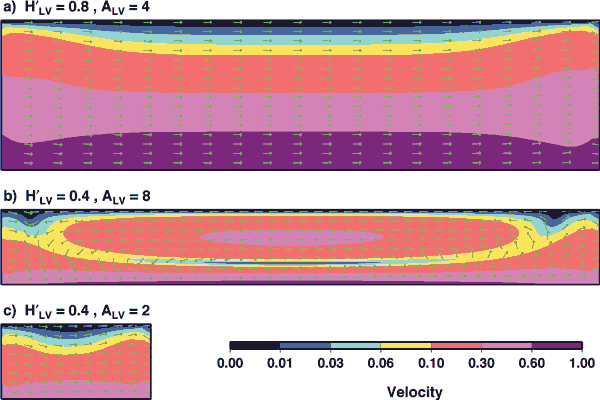
Figure 4: The flow field within
a low-viscosity “pocket” (as depicted
in Figure 2b) with viscosity h´=hLV/hasth=0.01
for three different choices of pocket aspect
ratio (ALV=WLV/HLV) and dimensionless height
H´=HLV/Hasth. Arrows show the flow field
direction, while colors present the magnitude
of flow. A pocket that is (a) tall (H´>0.7)
or (c) narrow (ALV<3) simply accommodates
asthenospheric shear without inducing significant
upwelling flow. Only within a wide pocket (ALV>6)
of intermediate thickness (0.2<H´<0.6),
as shown in (b), is circulatory flow, and thus
upwelling and volcanism, excited.
Tomographic studies of the asthenosphere
show low-velocity anomalies with a variety of geometries,
including some that could excite SDU [e.g., Humphreys & Dueker,
1994; Dueker et al., 2001; Moschetti
et al., 2007; van der Lee & Frederiksen,
2005]. Magnitudes of order -1.5% are typical, which,
if caused by thermal anomalies [Kohlstedt et
al., 1995] or hydration [Hirth & Kohlstedt,
1996], are consistent with a viscosity drop by
up to a factor of ~100. If asthenospheric source
rocks are close to solidus, we estimate that 1
cm/yr of upwelling can generate 2.5 km/Myr of melt
that is potentially eruptible. This is faster than
eruption rates observed at some locations of continental
basaltic volcanism [Conrad et al., 2010].
Conclusions
Most explanations for intraplate
volcanism invoke convection-related density heterogeneity:
small-scale convection, return flow from lithospheric “drips”,
edge-driven convection, and even plume impingement,
are examples of how density heterogeneity induces
upwelling flow. Here, we show that viscosity heterogeneity
can also drive upwelling flow, even in the absence
of any density heterogeneity, if it occurs in the
presence of vigorous asthenospheric shear. This
shear-driven upwelling (SDU) is fundamentally different
than the upwellings associated with convective
processes. As a result, SDU may provide a new explanation
for intraplate volcanism that occurs above rapidly
shearing asthenosphere. One current example may
be the basaltic volcanic fields of western North
America [Wannamaker et al., 2001], where
intraplate volcanism is difficult to explain via
other processes [Smith et al., 2002; Smith & Keenan,
2005] and the underlying lithosphere and asthenosphere
are laterally heterogeneous and appear to be shearing
vigorously [Humphreys & Dueker,1994; Zandt
et al., 1995; Dueker et al., 2001; Silver & Holt,
2002; van der Lee & Frederiksen, 2005; Conrad
et al., 2007].
Acknowledgements
We thank the Nevada Agency for
Nuclear Projects for support.
References
-
Ballmer, M.D., J. van
Hunen, G. Ito, P.J. Tackley, and T.A. Bianco,
Non-hotspot volcano chains originating from
small-scale sublithospheric convection, Geophys.
Res. Lett., 34, L23310,
doi:10.1029/2007GL031636, 2007.
-
Conrad, C.P., M.D. Behn,
and P.G. Silver, Global mantle flow and the
development of seismic anisotropy: Differences
between the oceanic and continental upper
mantle, J. Geophys. Res., 112, B07317,
doi:10.1029/2006JB004608, 2007.
-
Conrad, C.P., B. Wu, E.I.
Smith, T.A. Bianco, and A. Tibbetts, Shear-driven
upwelling induced by lateral viscosity variations
and asthenospheric shear: A mechanism for
intraplate volcanism, Physics of the
Earth and Planetary Interiors, 178,
162-175, 2010.
-
Dueker, K., H. Yuan, and
B. Zurek, Thick-structured Proterozoic lithosphere
of the Rocky Mountain Region, GSA Today, 11(12),
4-9, 2001.
-
Haxby, W.F., and J.K.
Weissel, Evidence for small-scale mantle
convection from Seasat altimeter data, J.
Geophys. Res., 91,
3507–3520, 1986.
-
Hernlund, J.W., P.J. Tackley,
and D.J. Stevenson, Buoyant melting instabilities
beneath extending lithosphere: 1. Numerical
models, J. Geophys. Res., 113,
doi:10.1029/2006JB004862, 2008.
-
Hillier, J.K., and A.B.
Watts, Global distribution of seamounts from
ship-track bathymetry data, Geophys. Res.
Lett., 34, L13304, doi:10.1029/2007GL029874,
2007.
-
Hirth, G., and D.L. Kohlstedt,
Water in the oceanic upper mantle: implications
for rheology, melt extraction and the evolution
of the lithosphere, Earth Planet. Sci.
Lett., 144, 93-108,
1996.
-
Humphreys, E.D., and K.G.
Dueker, Western U.S. upper mantle structure, J.
Geophys. Res., 99,
9615-9634, 1994.
-
King, S.D., A. Raefsky,
and B.H. Hager, ConMan: vectorizing a finite
element code for incompressible two-dimensional
convection in the Earth's mantle, Phys.
Earth Planet. Int., 59,
195-207, 1990.
-
King, S.D., and D.L. Anderson,
Edge-driven convection, Earth Planet.
Sci. Lett., 160, 289-296,
1998.
-
King, S.D., and J. Ritsema,
African hot spot volcanism: Small-scale convection
in the upper mantle beneath cratons, Science, 290,
1137-1140, 2000.
-
Kohlstedt, D.L., B. Evans,
and S.J. Mackwell, Strength of the lithosphere:
constraints imposed by laboratory experiments, J.
Geophys. Res., 100,
17587-17602, 1995.
-
Le Pourhiet, L., M. Gurnis,
and J. Saleeby, Mantle instability beneath
the Sierra Nevada mountains in California
and Death Valley extension, Earth Planet.
Sci. Lett., 25, 104–119,
2006.
-
-
Moschetti, M.P., M.H.
Ritzwoller, and N.M. Shapiro, Surface wave
tomography of the western United States from
ambient seismic noise: Rayleigh wave group
velocity maps, Geochem. Geophys. Geosyst., 8,
Q08010, doi:10.1029/2007GC001655, 2007.
-
Pakdel, P., S.H. Spiegelberg,
G.H. McKinley, Cavity flows in Elastic liquids:
Two-dimensional flows, Phys. Fluids, 9,
3123-3140, 1997.
-
Phipps Morgan, J., Thermodynamics
of pressure release melting of a veined plum
pudding mantle, Geochem. Geophys. Geosyst., 2,
2000GC000049, 2001.
-
Raddick, M.J., E.M. Parmentier,
and D.S. Scheirer, Buoyant decompression
melting: A possible mechanism for intraplate
melting, J. Geophys. Res., 107(B10),
2228, doi:10.1029/2001JB000617, 2002.
-
Shankar, P.N., and M.D.
Deshpande, Fluid mechanics in the driven
cavity, Ann. Rev. Fluid Mech., 32,
93-136, 2000.
-
Shen, C., and J.M. Floryan,
Low Reynolds number flow over cavities, Phys.
Fluids, 28, 3191-3202,
1985.
-
Silver, P.G., and W.E.
Holt, The mantle flow beneath western North
America, Science, 295,
1054-1057, 2002.
-
Smith, E.I., and D.L.
Keenan, Yucca Mountain could face greater
volcanic threat, EOS Transactions of
the American Geophysical Union, 86,
317-312, 2005.
-
Smith, E.I., D.L. Keenan,
and T. Plank, Episodic volcanism and hot
mantle: Implications for volcanic hazard
studies at the proposed nuclear waste repository
at Yucca Mountain, Nevada, GSA Today, 12,
4-10, 2002.
-
van der Lee, S., and A.
Frederiksen, Surface wave tomography applied
to the North America Upper Mantle, in "Seismic
Earth: Array Analysis of Broadband Seismograms",
Eds: G. Nolet and A. Levander, Geophysical
Monograph Series, 157,
67-80, 2005.
-
van Hunen, J., and S.
Zhong, Influence of rheology on realignment
of mantle convective structure with plate
motion after a plate reorganization, Geochem.
Geophys. Geosyst., 7,
Q08008, doi:10.1029/2005GC001209, 2006.
-
van Wijk, J., J. van Hunen,
and S. Goes, Small-scale convection during
continental rifting: Evidence from the Rio
Grande rift, Geology, 36,
575-578, 2008.
-
Wannamaker, P.E., J.M.
Bartley, A.F. Sheehan, C.H. Jones, A.R. Lowry,
T.A. . Dimitru, T.A. Ehlers, W.S.Holbrook,
G.L. Farmer, M.J. Unsworth, D.B. Hall, D.S.
Chapman, D.A. Okaya, B.E. John, and J.A.
Wolfe, The Great Basin-Colorado Plateau transition
in central Utah: An interface between active
extension and stable interior, in The
Geological Transition: Colorado Plateau to
Basin and Range, Erskine, M.C., J.E.Faulds,
J.M. Bartley, and P. Rowley (Eds.), UGA/AAPG
Guideb. 30/GB78, 1-38, 2001.
-
West, M., J. Ni, W.S.
Baldridge, D. Wilson, R. Aster, W. Gao, and
S. Grand, Crust and upper mantle shear wave
structure of the southwest United States:
Implications for rifting and support for
high elevation, J. Geophys. Res., 109,
B03309, doi:10.1029/2003JB002575, 2004.
-
Zandt, G., S.C. Myers,
and T.C. Wallace, Crust and mantle structure
across the Basin and Range–Colorado
Plateau boundary at 37°N latitude and
implications for Cenozoic extensional mechanism, J.
Geophys. Res., 100,
10529–10548, 1995.
last updated
20th February, 2010 |
